Farb and Friends

Farb and Friends is a low-stakes, informal seminar for graduate students and postdocs to share expository talks on topics adjacent to geometry and topology.

Spring 2025

Title Speaker Date
Intro to complex reflection groups We will discuss the Shephard-Todd classification of finite irreducible complex reflection groups, and how one can think about these groups visually.
Isabelle Steinmann 04/04
Euclidean Scissors Congruence Two polytopes \(P\) and \(Q\) are scissors congruent if one can be decomposed into finitely many polytopes which can be rearranged to obtain the other. In 2-dimensions, two polygons are scissors congruent if and only if they have the same area. We will focus on the analogous question in \(\mathbb{R}^3\) : what conditions are necessary and sufficient to ensure scissors congruence of polyhedra? If time permits, we will also discuss the set up of the problem in higher dimensions.
Reena Somani 04/11
Mapping tori of expanding maps Expanding maps on compact nilmanifolds are fundamental objects of study in both dynamics and geometric group theory. The fundamental group of the mapping torus of such a map has rich (coarse) geometry, combining that of negatively curved homogeneous manifolds and trees. In this talk, I will first discuss some classical results surrounding expanding maps on nilmanifolds, then present recent work which says (roughly) that a group with similar coarse geometry to the aforementioned examples must come from an expanding map on a nilmanifold. This result parallels classical work of Gromov, Shub, Franks and Heintze.
Noah Caplinger 04/18

Previous Quarters

Winter 2025
Title Speaker Date
Polynomial spaces as CW complexes We’ll see how polynomial spaces deformation retract to some cool CW-complexes which offer a nice way to visualize them. This is tied to what’s been going on in Benson’s class + the last pre-Christmas G&T seminar + some of my previous Farb & Friends talks (no need to have seen / understood any of the above though). As in any good GGT talk, we will have lots of pretty pictures.
Chloé Postel-Vinay 10/11
Automorphism groups of isometries Isometry groups of geometric spaces show up all across math. In this talk I will explain a fairly general strategy to compute them. My final example will be a geometric proof that \( \mathbb{P}\mathrm{SL}(2,\mathbb{R}) \) has no outer automorphism.
Noah Caplinger 01/24
Fundamental group of the complement of a plane algebraic curve I will tell you how to write down a presentation of \( \pi_1 \) of the complement of a plane algebraic curve, à la Zariski and van-Kampen, and discuss some intriguing examples. In principle this will imbue you with the power to compute \( \pi_1 \) of an arbitrary hypersurface complement in affine or projective space.
Peter Huxford 01/31
Ivanov's Conjecture, the Putman-Wieland Conjecture, and Character Varieties. This talk will focus on three parallel stories, 1) Ivanov's conjecture, which states that in genus at least three all finite-index subgroups of the mapping class group have trivial abelianization. 2) The Putman-Wieland conjecture, which concerns (virtual) mapping class group representations for a surface \(S\) arising from the homology of a cover \(S' -> S\). 3) Dynamics of Mapping Class Groups on Character Varieties: that is how \(\mathrm{Mod}(S)\) acts on the variety \( \mathrm{Hom}(\pi_1(S), GL_n\mathbb{C})//GL_n \mathbb{C} \), which parameterizes flat complex vector bundles of rank n (equivalently local systems of rank n). The bulk of the talk will be devoted to the exposition of these three topics and how they relate to one another (for example, the equivalence of Stories 1 and 2). If time permits we will also discuss recent work of Lam-Landesmann-Litt which leverages the arithmetic of Story 3 to provide strong results for conjectures 1 and 2.
Faye Jackson 02/07
Knot surgeries and exotic 4-manifolds In 1998, Fintushel—Stern introduced a construction called knot surgery which takes certain smooth 4-manifolds \(M\) and knots \(K\) (in \(S^3\)) and produces smooth 4-manifolds that are homeomorphic but not diffeomorphic to \(M\). In this talk, I will describe this procedure for \(M = E(1)\), the rational elliptic surface, and fibered knots \(K\), and hopefully convince you that the resulting 4-manifolds \(E(1)_K\) are homeomorphic but not diffeomorphic to \(E(1)\). Along the way, we will encounter Lefschetz fibrations, the symplectic Thom conjecture, and Freedman's classification of closed, simply-connected, topological 4-manifolds.
Seraphina Lee 02/14
One circle to rule them all... Given a two-dimensional foliation of a 3-manifold with hyperbolic leaves, the fundamental group \(\pi_1(M)\) has a natural action on a space of many circles. These are the circles at infinity of the leaves in the foliation of the universal cover of \(M\). A universal circle binds these circles together and gives an action on a single circle instead. In this example-heavy talk, we will learn how to construct a universal circle for taut foliations and see how universal circles relate to modern research directions in 3-manifold topology.
Fran Herr 02/21
Low-dimensional reps of mapping class groups Mapping class groups of surfaces are this mysterious little thing that we know so much and yet so little about. Linear algebra, on the other hand, is our beloved friend and a very useful hammer in cracking open mathematical nuts. In this talk, I will talk about what happens when we (i.e., Korkmaz and Kasahara) take this hammer and whack it against mapping class groups.
Zhong Zhang 02/28

Fall 2024
Title Speaker Date
Homogeneous manifolds of negative curvature Riemannian manifolds of variable negative curvature are scary. To make them nicer, assume they are homogeneous(= isometry group is transitive). Still seems scary. In this talk, I will present a theorem of Heintze which says this setup isn't scary at all: every homogeneous, simply connected manifold of (possibly variable) negative curvature is isometric to a Lie group with a left-invariant metric.
Noah Caplinger 10/11
Construcing zippers Everyone has seen a zipper. It is a pair of two objects that one tangles with the other to fill in gaps. But how would a mathematical object called zipper look like? I will try to answer this question while talking about the ends of a space, circular orders and of course 3-manifold group actions on \( S^2\).
Ino Loukidou 10/25
Groups acting on trees I will talk about the structure theorem for groups acting on trees, sometimes called "Bass-Serre theory".
Noah Caplinger 11/01
Spectral sequences in everyday life Spectral sequences appear in many places in mathematics, including algebraic topology, algebraic geometry, and geometric group theory. We will discuss several different common types of spectral sequences and explain how to use them in practice. This talk will be mostly examples.
Dan Minahan 11/08
The genus function for four manifolds The minimal genus problem asks to compute the minimal genus of a smoothly embedded surface representing a given 2-homology class. We will discuss some rudimentary techniques, e.g blowing-up, to attack this problem. Then by quoting some big hammers coming from Seiberg-Witten theory, we will compute the minimal genus for classes in \( \mathbb{P}^2 \) and \(\mathbb{P}^1 \times \mathbb{P}^1\). A digression on the happy case of 3-manifolds might be also given.
Carlos A. Serván 11/15
Some families of abelian varieties You may have seen double cosets like "\(\Gamma \backslash G/ K\)" appear in various settings. For example, the modular curve can be written as \( SL_2(\mathbb{Z}) \backslash SL_2(\mathbb{R}) / SO_2(\mathbb{R})\). In this talk, we'll explicitly describe how to realize some families of abelian varieties as expressions of this form. Time permitting, we'll explain how this machinery shows that the quotient of the upper half-plane modulo the (2,3,7)-triangle group (more or less) parameterizes abelian varieties which are some of the simplest open cases of the Mumford-Tate and Hodge conjectures.
Abhijit Mudigonda 11/22
Stayin' Alive with BGs We will briefly review the theory of principal G-bundles and discuss classifying spaces BG. We will then analyze some examples and their cohomology through the lens of obstruction theory.
Tobias Shin 11/29

Spring 2024
Title Speakers Date
The modular flow and the Rademacher invariant In 2006 Étienne Ghys gave a ICM talk, with corresponding proceedings article Knots and Dynamics (2007). There he discusses the following situation, which I will attempt to recount. The space of unit area lattices in C is homeomorphic to S^3 - trefoil. On this space there is a flow, called the modular flow. Given a hyperbolic matrix A in SL(2,Z), we can produce a periodic orbit of this flow. Ghys proves that the linking number of this periodic orbit with the removed trefoil can be computed via the Rademacher invariant of A, which is a special function SL(2,Z) -> Z. This invariant has many equivalent definitions, one for example is closely related to the Dedekind eta function whose 24th power is a modular form of weight 12.
Peter Huxford 04/19
Centralizer of braids After recalling some results about classification of braids, I will proceed to explain a result of González-Meneses and Wiest about computing the centralizer of a braid.
Chloé Postel-Vinay 04/05
Obstruction theory (for kids) We will discuss basic obstruction theory and draw some fundamental pictures from high-dimensional algebraic and differential topology. For example, one can ask the question: what does a cycle representing a homology class look like? We will also see how Thom answers this question completely, while revealing a deep relationship between differential manifolds (modulo a homology relation) and homotopy groups of spheres.
Tobias Shin 03/29

Winter 2024
Title Speakers Date
Finite irreducible reflection groups We will prove the classification of finite irreducible reflection groups and, if we have time, we will show that the classification of regular convex polytopes is a corollary of this. The proof will involve root systems, Coxeter groups and Dynkin diagrams.
Isabelle Steinmann 03/01
Kleinian surface groups The classification of hyperbolic 3-manifolds was one of the main themes of geometric topology for 50 years. Some of the biggest remaining questions were finished off relatively recently, by Perelman (geometrization), Agol (virtual fibering), and Minsky (ending laminations). In this talk, I’ll tell you a bit about the story of hyperbolic 3-manifolds homotopy equivalent to surfaces, hopefully getting to a statement of the ending lamination theorem. No background will be required (other than basic hyperbolic geometry) and no proofs will be given.
Aaron Calderon 02/09
3-manifolds and the L-space conjecture I will talk about some background on 3-manifold topology, triangulations, Dehn surgeries, heegaard splittings and hyperbolic structures (maybe even a little about other geometric structures because they are cool). Then, I'll discuss the L-space conjecture and (some of) the terms involved separately.
Ino Loukidou 02/02
Classifying Foliations In order to classify vector bundles over a base space, one can consider homotopy classes of maps from the base space to the classifying space of the orthogonal group. Similarly, in order to classify bundles, one considers homotopy classes of maps from the base space to the classifying space of a homeomorphism group. In this talk, I will discuss Haefliger's work on how one can classify foliations on a manifold.
Oliver Wang 01/26
Using (total) symmetry to study homomorphisms I will talk about a relatively new technique for studying homomorphisms between groups which Farb and his Friends frequently find fascinating. It has a high ratio of (useful/powerful consequences) : (difficulty to learn). The first part of the talk will be on this "blueprint" for studying homomorphisms, initially developed by Dan Margalit. Time permitting, I will discuss my work with Nick Salter on classifying the maximal totally symmetric sets in GLn(C), thereby giving an avenue towards studying representations of groups admitting large totally symmetric sets.
Noah Caplinger 01/19
Springer fibers and irreps of the symmetric group In 1976, Springer showed that the cohomology of certain subvarieties of the flag variety carries an action of the symmetric group \(S_n\) and that every irrep of \(S_n\) appears exactly once in his construction. I will state his theorem precisely, try to convince you that the action does not come from an \(S_n\) action on the varieties themselves, and give a construction of this action.
Linus Setiabrata 01/12

Fall 2023
Title Speakers Date
On the homotopy type of compact kähler manifolds Carlos A. Serván 11/17
Wall’s stabilization theorem In 1964, Wall proved that any pair of homotopy-equivalent closed, oriented, simply-connected, smooth 4-manifolds become diffeomorphic after taking connected sums with \( k(S^2 × S^2) \) for some \(k \geq 0\). In this talk, I will outline some main steps of Wall’s proof using h-cobordisms. I will also survey some recent stabilization results in other smooth 4-dimensional contexts.
Seraphina Lee 11/10
Dual Artin Groups In this talk I will briefly review the definitions of Artin and Coxeter groups and move on to explain what dual Artin groups are, how to construct them, and how their study can help our understanding of Artin groups.
Chloé Postel-Vinay 11/03
Biases between Congruence Classes for Parts in Partitions In this talk we'll discuss how the parts of partitions of n are distributed among congruence classes r mod t for some fixed t. In particular, we will give an asymptotic formula for this quantity for k-indivisible partitions. This asymptotic's first-order term does not depend on the congruence class; however, the second order term displays a bias towards certain congruence classes. This bias is chaotic, and produced by a strange twist and scaling action on the digamma function. This links our story to the world of L-functions and Galois representations, making otherwise impossible questions about the bias tractable. We will also discuss some subset of
  1. The lack of combinatorial proofs in this area, despite numeric evidence that the results hold for \( n\geq 8 \)
  2. A variety of unsolved questions about the biases which seem utterly intractable and yet utterly interesting.
  3. Linear independence of rational values of the digamma function.
Faye Jackson 10/20
What sort of space is a complex algebraic variety? Complex algebraic varieties are not always manifolds. But what are they? The purpose of this talk is to describe some work of Milnor, Hironaka, Lê, and others, on the topological type of a variety with singularities. There are some fun results:
  • varieties are pseudomanifolds
  • exotic spheres can show up in the topology of algebraic varieties!
  • isolated singularities give rise to fibered knots!
  • Lê's fibration theorem (which is one road to perverse sheaves)
Singularity theory is a very detail heavy subject, so the focus will be on showing off some of the main theorems with interesting (to me, at least) examples, rather than giving complete proofs of the foundational results.
Michael Barz 10/13
Holomorphic maps between configuration spaces For a Riemann surface \(X\), let \(Conf_n(X)\) be the space of n-element subsets of X. I will be discussing the following open question.
What are the holomorphic maps \( Conf_n(X) \to Conf_m(Y)\)?
This question is interesting to me because there are several exceptional algebro-geometric constructions that give rise to holomorphic maps, and any answer to this question has to "see" these special constructions. Certain special cases of this question have been answered by Lin almost 20 years ago. More recently this question has inspired several interesting conjectures (of Farb), and several theorems (of friends). I will discuss some of these, including the recent work of Chen and Salter, as well as myself and Schillewaert, on the problem.
 Peter Huxford 10/06

Spring 2023
Title Speakers Date
High Dimensional Knots A knotted sphere is an isotopy class of embeddings of \(S^n\) in \(S^{n+k}\) and the set of such isotopy classes forms an abelian group under connect sum. When \(k>2\), the Zeeman unknotting theorem states that all embeddings are topologically unknotted. Smoothly, this is not the case. I will discuss works of Haefliger and Levine which show that these groups fit in exact sequences from which we can obtain computations.
Oliver Wang 3/29
Kähler groups Let \( X \) be a compact Kähler manifold, and \( G = \pi_1(X). \) \( G \) is then called a Kähler group. I would describe simple examples of Kähler groups, all of which actually are fundamental groups of smooth projective varieties, and a variety of obstructions for an arbitrary, finitely presented group to be Kähler.
Carlos A. Serván 4/5
An unusual subgroup of the mapping class group In this talk I will present an infinite index subgroup of the mapping class group that is:
  • Finitely generated by Dehn twists
  • Virtually surjects onto \( {\rm Sp}(2g,\mathbb{Z}) \)
  • whose intersection with the Torelli group virtually surjects onto \( \Lambda^3 H/ H \)
  • Contains framed mapping class group of large genus subsurfaces.
 Ishan Banerjee 4/12
Plücker formulas Let \( C = V(f) \) be a curve in the complex projective plane. I will define the dual curve \( C^* \) of \( C \) and discuss the Plücker formulas, which impose conditions on the numbers of nodes and cusps of \( C \) by relating them to the number of nodes and cusps of \( C^* \) and the degrees of \( C \), \( C^* \).
Peter Huxford 4/19
Genus of a surface in \(\mathbb{CP}^2\) The genus of a smooth, degree-\(d\) algebraic curve in \(\mathbb{CP}^2\) is \(\frac 12 (d-1)(d-2)\). The Thom conjecture, proven by Kronheimer and Mrowka in 1994, says that such curves achieve the minimal genus among all smoothly embedded surfaces in its homology class. However, there exist topologically embedded surfaces which are homologous to smooth, degree-\(d\) algebraic curves but have genus smaller than \(\frac 12 (d-1)(d-2)\). In this talk, we will discuss Rudolph's construction of topologically locally-flatly embedded surfaces in \(\mathbb{CP}^2\) of genus strictly less than that of a homologous smooth algebraic curve.
Seraphina Lee 4/26
Failure of Hodge Symmetry in Characteristic p. If \(X/C\) is a smooth projective complex variety, it follows from Hodge theory that X satisfies “Hodge symmetry”; i.e. that the cohomology groups \(H^{p,q}(X)\) and \(H^{q, p}(X)\) have the same dimension. However, in 1958, Serre showed by constructing an example that Hodge symmetry need not hold for varieties over fields of positive characteristic. In this talk we will explain Serre’s example and discuss a more modern perspective on it which illustrates the general principle that quotients by a group action share the same properties as the classifying space of that group.
Casimir Kothari 5/3
Toys we play with during grad(e) school We will discuss "__". Ongoing attempts to understand __ will lead to connections between the following topics which will mention:
  1. Real roots and signs of coefficients of polynomials parametrizing combinatorial objects
  2. Combinatorics vs. topology of linear subspace arrangements
  3. Controlling singularities on families of varieties
What is "__"? The title gives a hint.
Soohyun Park 5/10

Winter 2023
Title Speaker Date
Cayley Bacharach sets lie on curves In this talk I will briefly discuss what Cayley Bacharach sets are. I will describe a few classical examples of Cayley Bacharach sets. I will then give a proof of a theorem of mine that states under certain hypotheses Cayley Bacharach sets all lie on low degree curves.
Ishan Banerjee 1/4
Smooth Models for Certain Partially Hyperbolic Systems We prove that under restrictions on the fiber, any fibered partially hyperbolic system over a nilmanifold is leaf conjugate to a smooth model that is isometric on the fibers and descends to a hyperbolic nilmanifold automorphism on the base.
Meg Doucette 1/11
Bogomolov-Tschinkel's construction We will explain Bogomolov-Tschinkel's theorem that any hyperelliptic curve has an unramified cover mapping to the curve \(y^2 = x^3 + 1\). Their construction was motivated by potential applications to uniform bounds on the number of rational points on hyperelliptic curves. Their theorem also has applications to the Putman-Wieland conjecture about fixed vectors under a certain action of the mapping class group, and Prill's problem asking whether there is a cover of a curve of genus at least 2 so that every fiber moves in a pencil.

Note: This was a special talk held in place of the regular Farb and Friends meeting this week.
Aaron Landesman (Harvard) 1/18
Symmetries unifying the continuous and discrete We discuss fascinating recent work in combinatorics exploiting symmetries inspired by results/conjectures in algebraic geometry/topology. This often involves combinatorial/analytic representations of properties exhibited by cohomology groups. Examples of interesting and effective applications include questions on unimodality or log concavity (e.g. chromatic polynomials) and deep symmetries underlying problems motivated by plane geometry questions.
Soohyun Park 1/25
Sturm’s Root Counting Theorem and Two Reformulations This is a sideline history talk.
In the 1820’s, Sturm stated a theorem on the number of real roots of a real polynomial on an interval. Several decades later, Sylvester gave it a linear algebraic reformulation, which subsequently bore an algebraic reformulation, in the setting of the Witt group of \(\mathbb{R}(X)\).
Peng Hui How 2/1
A K(pi, 1) for the braid group Following work by Brady and McCammond, I will explain how to construct a simplicial complex which is a K(pi,1) for the braid group Bn. It arises from a free group with generators in a poset of Sn. I will explain a nice way to visualize those generators, and draw some pictures for the audience. If time permits, I will give a summary of the proof of the contractibility of the universal cover.
Chloé Postel-Vinay 2/8 at 4:10pm
Fair division and peg problems We survey some results in the theory of fair division, where one wants to evenly divide many things using relatively few operations. These results can be proven from the Borsuk-Ulam theorem and its friends. We apply fair division results to variants of the square peg problem: specifically, we'll show that every loop in the plane inscribes infinitely many rectangles and that every loop in 3-space inscribes infinitely many parallelograms.
Linus Setiabrata 2/15
Building random hyperbolic surfaces What does it mean to pick a “random” hyperbolic surface, and how does one even go about “picking” one? Mirzakhani gave an inductive answer to this question by gluing together smaller random surfaces along long curves. Reformulating this procedure as studying the equidistribution of certain sets inside moduli space allows us to invoke a powerful analogy between Teichmüller theory and homogeneous dynamics. In this talk, I’ll explain this analogy and give an overview of Mirzakhani’s proof; if time permits, I’ll also mention some recent developments that give a much broader framework for these results.
Aaron Calderon 2/22

Fall 2022
Title Speaker Date
The dynamics of iterated fiber products You can make a dynamical system out of almost anything. For example, I'll show how to make a dynamical system out of branched covers of the projective line using rational functions. We'll use a little algebra and topology to analyze the orbits of these systems, concluding with a satisfying dichotomy. If time permits, I'll explain how this relates to an "arithmetic dynamical Mordell-Lang" result I proved with Mike Zieve.
Trevor Hyde 10/5
Kneser graphs and spheres In 1956, Kneser gave a conjectural formula for the chromatic numbers for a family of graphs now known as Kneser graphs. This purely combinatorial conjecture was first resolved by Lovász in 1978 using topological methods. In this talk, I will give a proof outline and if time permits, hint towards its many variations.
Seraphina Lee 10/12
When can circle bundles be flat? An oriented circle bundle is flat if the total space admits a codimension one foliation that is transverse to the fibers. I will discuss a classic result known as the Milnor–Wood inequality, which states that for such a bundle over a closed oriented surface of genus g > 0, one must have |e| ≤ 2g - 2, where e is the Euler number of the bundle.
Peter Huxford 10/19
The Drinfeld Curve The complex irreducible characters of the finite group SL_2(F_q) were constructed long ago. These fall into two categories: the principal series, where it is easy to write down matrices defining an action, and the discrete series, where it is not so easy. Remarkably, Drinfeld discovered at age 19 that the discrete series representations can be constructed using étale cohomology of a certain curve. We will explore this remarkable geometric construction.
Joshua Mundinger 10/26
Using Morse theory to construct minimal surfaces In the 80s, Yau conjectured the existence of infinitely many minimal surfaces in any 3-manifolds. This conjecture was solved in recent years using min-max theory, which is some version of infinite dimensional Morse theory. I will briefly talk about the ideas behind.
Adrian Chu 11/2
Symplectic packings and Nagata's conjecture on curves Let \(N \geq 9\) and \(p_1, p_2, \ldots, p_N\) be very general points in \(\mathbb{C}P^2\). Nagata's conjecture predicts a bound on the degree of any curve \(C\) passing through all points \(p_i\) in terms of its multiplicity at each \(p_i\). On the other hand, a symplectic packing of \(\mathbb{C}P^2\) by \(N\) balls of radius \(\lambda\) is a symplectic embedding of \(N\) disjoint balls, each of radius \(\lambda\), into \(\mathbb{C}P^2\). In this talk I will explain how these seemingly unrelated topics are actually very intimately related.
Carlos A. Serván 11/9 at 3pm
Redundancies of polynomial conditions and Lefschetz properties We consider different perspectives on points which do *not* impose independent conditions on the space of polynomials of a given degree. Apart from having interesting combinatorial analogues, some of the most "degenerate" combinatorial cases have close connections to (analogues of) Lefschetz properties.
Soohyun Park 11/16
Smooth structures on high dimensional manifolds I will describe how to classify smooth structures on manifolds of dimension at least 5. A consequence of this classification is that there are only finitely many smooth manifolds homeomorphic to a given closed topological manifold of dimension at least 5. If there is time, I will discuss some other applications.
Oliver Wang 11/30

Spring 2022
Title Speaker Date
Bialgebraic geometry, first order logic and Grothendieck's dream Consider your favorite algebraic variety with infinite fundamental group (I like C^* or maybe even (C^*)^n). Sometimes, it happens that the universal cover is itself an algebraic variety and bialgebraic geometry asks the question: Which algebraic varieties in the universal covering have an algebraic variety as image under the covering map? In general, this question is very hard even in simple cases. We will discuss some basic examples and the kinds of methods that are used to study this question. This will lead us to a seemingly very unrelated topic: First order logic. On the way we might even find a realization of Grothendieck's dream of “tame topology”, a theory of topological spaces avoiding unwanted pathologies such as space-filling curves and spaces with infinitely many connected components.
Frederik Benirschke 5/23
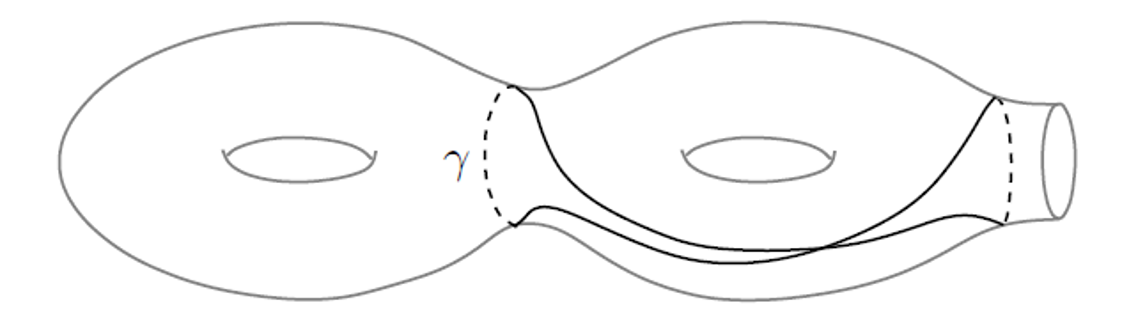
Bounding immersed loops by immersed surfaces Which of the following immersed circles on the plane bound *immersed* disks? This turns out to be a complicated problem in general. What about the analogous problem of bounding immersed loops on a higher genus surface by immersed surfaces (see the last figure for an example)? A stable version of this problem turns out to have a clean answer, using hyperbolic geometry and a few related invariants (rotation number, stable commutator length). I'll explain this work of Calegari.
Lvzhou Chen (UT Austin) 5/16
Etale cohomology I have been blackboxing etale cohomology for a long time, simply thinking of it as singular cohomology with a Galois action. In this talk, I will try to explain how etale cohomology is closely related to the Galois action. For example, the etale cohomology of a field is the same as its Galois cohomology. Then I would like to explore a bit why etale cohomology, in contrast to sheaf cohomology on Zariski sites, yields the correct Betti numbers by examples. I would say a few words about Galois representations coming from etale cohomology.
Chengyang Bao 5/9
A boring dynamical system and why it's so interesting A couple years ago I noticed an interesting way to build a dynamical system on the space of unordered configurations of 3 points in the plane. To my chagrin, this turned out to be a boring dynamical system. However, it's boring for a very interesting reason! In this talk you'll get configuration spaces, elliptic curves in pencils, tetrahedra, torsion, and more. This talk may not be for everyone, but it may be just right for you.
Trevor Hyde 5/2
Boundaries of Groups and Cohomology There are several notions of boundaries of groups. For instance, given a Gromov hyperbolic group, one can define the Gromov boundary as equivalence classes of geodesic rays. I will explain a theorem of Bestvina and Mess relating the cohomology of this space to the cohomology of the group. Another notion of boundary is the Poisson boundary, which arises from probability theory. If there is time, I will try to convince you that this boundary should also give us cohomological information.
Oliver Wang 4/25
The Simpson Twistor In this talk, I'll present a perspective on Hodge theory due to Simpson. It turns out there is a certain scheme over R, the twistor curve, that encodes much of the information relevant to Hodge theory. Topologically, this curve looks like the real projective plane. I'll explain an equivalence of categories between pure real Hodge structures of weight n and U(1)-equivariant vector bundles of slope n/2. Further, it turns out that forgetting the U(1)-action relates to an interesting category of real isocrystals which in odd weights is equivalent to quaternionic vector spaces. If time permits, I'll mention (without getting into technical details) some fascinating similarities and differences with the p-adic setting, which is how I got interested in this topic.
Gal Porat 4/18
Approximate subgroups in Lie groups We will discuss the notion of approximate groups in Lie groups and their relation to nonperiodic tilings of \(mathbb{R}^n\) or hyperbolic space and discuss recent results of Simon Machado regarding approximate subgroups in Lie groups of higher rank.
Sebastian Hurtado-Salazar 4/11
Quartic curves and K3 surfaces I will talk about my recent work regarding the computation of the monodromy of the family of K3 surfaces branching over smooth quartic curves. I hope to elucidate the beautiful interplay between many objects, including:
  • 27 lines on a cubic surface
  • 28 bitangents to a quartic curve
  • Degree 2 del Pezzo surfaces
  • Weyl groups and graph automorphisms
  • Hodge and cyclic decompositions
  • Lattices and gluing groups
  • Moduli spaces and framings
  • The Torelli theorem for K3 surfaces
 Adán Medrano Martín Del Campo 4/4

Winter 2022
Title Speaker Date
On homological stability for discriminant complements and related spaces I will survey homological stability for discriminant complements, discussing some results and open questions.
Ishan Banerjee 3/7
Peg Problem

Given a Jordan curve on the plane, can you always find 4 points that they form a rectangle, or even a square? What about other shapes? What about an imbedded 2 sphere in \(\mathbb{R}^3\), can you find similar statement? This presents work of Cole Hugelmeyer, Josh Greene and Andrew Lobb.

Lei Chen (UMaryland) 2/28
Orthoschemes

I will talk about a forgotten theorem of Coxeter, which gives a generalization of Gauss’s Pentogramma Mirificum. I will explain its role in the Goncharov Program and say a few words about its role in the proof of the theorem of Böhm on volumes of hyperbolic polytopes.

Daniil Rudenko 2/21
Invariant random subgroups and asymptotic invariants

Let \(M\) be a closed aspherical manifold with the fundamental group \(\Gamma\). Suppose we are interested in the growth of topological invariants of a sequence of finite covers \(M_n\) of \(M\). These can be often read from the limit objects which are constructed using the sequence \(M_n\). One way of doing it is by considering the weak-star limits of normalized counting measures supported on the conjugates of the fundamental group of \(M_n\) inside the space of subgroups of \(\Gamma\). The limit is a random subgroup whose distribution is invariant by conjugation by \(\Gamma\) - we call them "invariant random subgroups”. I my talk I will explain how they can be applied to various problems in geometry and how they fit in the more general framework of unimodular measures on moduli spaces.

Recording   Notes
Mikolaj Fraczyk 2/14
Iterated monodromy groups and finite automata

Given a rational function f(x) with complex coefficients, the iterates of f(x) determine a sequence of finite degree branched covers of the sphere. Finite branched covers of the sphere are essentially determined by their monodromy, so it stands to reason that the dynamics of f(x) should be encoded in this sequence of monodromy groups. But how exactly does that work? In this talk I'll introduce the notion of an iterated monodromy group, show how this leads us by the nose to the important concept of a post-critically finite map, and see how this relates to finite automata acting on infinite trees.

Trevor Hyde 2/7
Sextic curves with six cusps

There are two kinds of sextic curves C in P^2 with exactly six ordinary cusps and no other singularities: one kind has \(\pi_1(\mathbb{P}^2 - C) = \mathbb{Z}/2 * \mathbb{Z}/3\) non-abelian, and the other has \(\pi_1(\mathbb{P}^2 - C) = \mathbb{Z}/6\) abelian. These two kinds of curves are distinguished by whether or not the six cusp points lie on a conic. This is very weird and has confused me for a long time. I'm going to talk about these sextics, some cool things, some weird things, and some things that still confuse me about all this.

Peter Huxford 1/31
Polynomial equations in groups

I will discuss a notion of polynomial equations in groups motivated by a question about enlarging a group by adding a generator. Then I will explain why unitary groups are "algebraically closed".

Recording
Nate Harman (UMich) 1/24

Fall 2021
Title Speaker Date
Prym varieties

The Prym construction associates a principally polarized abelian variety of dimension \(g-1\), referred to as the Prym variety of the cover, to a double cover \(f: Y \to X\) of a smooth genus \(g\) curve. I will discuss some interesting properties of this construction.

Carlos Marcelo Servan 12/6
\(\text{Out}(S_6)\) and Pascal's Mysticum

I'll discuss a fun (and the historically original) appearance of an outer automorphism of \(S_6\) by fussing around with hexagons on conic plane curves. Along the way we meet up with Steiner, Plücker, Salmon, Kirkman, Cayley, Bacharach, Braikenridge, Maclaurin, and of course Pascal.

Michael Klug 11/29
Involutions in the plane Cremona group

The plane Cremona group \(\text{Cr}(2)\) (over \(\mathbb C\)) is the group of birational automorphisms of \(\mathbb{CP}^2\). There is a classification of the conjugacy classes of order \(2\) elements of \(\text{Cr}(2)\) into three types: de Jonquières, Geiser, and Bertini. In this talk, I will describe these three types of involutions explicitly.

Seraphina Lee 11/15
Solving Equations with Dynamics

It is well-known that there is no general solution by radicals for polynomials of degree at least 5...but are there other ways to solve polynomial equations? In this talk I will discuss the possibility of finding polynomial roots through iteration of rational functions. We will see, following McMullen, that iteration allows us to solve the general quintic (and not much else!)

Trevor Hyde 11/8
Mednykh's Formula

Mednykh's formula counts homomorphisms from the fundamental group of a surface to a finite group \(G\) in terms of the representation theory of \(G\). We'll discuss two proofs of this formula, as well as related questions.

Joshua Mundinger 11/1
Mapping class groups of connected sums of \(S^2 \times S^1\)

Recently Bruno Zimmermann posted a short paper on the Nielsen realization problem for the mapping class groups of the three-manifolds formed by taking finite connected sums of \(S^2 \times S^1\). This made me curious about what is known about these groups! I will survey some of what I found out and will also discuss some of the results and arguments in Zimmermann’s paper.

Justin Lanier 10/25
Linear subspaces on a Fano \(k\)-plane invariant class of varieties

Consider the following statement: "The space of \(k\)-planes contained in varieties in \(A\) is in \(A\)." What can \(A\) be? For a certain \(A\), this will depend on a special property of varieties represented by points of \(A\).

Soohyun Park 10/18
What's so special about the homology of algebraic varieties?

It turns out that the (co)homology groups of an algebraic variety admit a number of amazing structures, which go beyond the homology of ordinary topological spaces. I will talk about several of these structures, how they reflect the "rigidity" of algebraic geometry, and about several deep analogies/conjectures connecting them.

Phil Tosteson 10/11

Spring 2021
Title Speaker Date
Groups acting on graphs

Group actions on graphs reveal information about the group itself. We demonstrate this on SL(2,Z) and its various generalizations. For example, we show that mapping class groups of surfaces with positive genus is finitely generated by Dehn twists.

Recording   Notes
Peng Hui How 6/7
Stable torsion length

The stable torsion length in a group is the stable word length with respect to the set of all torsion elements. We show that the stable torsion length vanishes in crystallographic groups. We then give a linear programming algorithm to compute a lower bound for stable torsion length in free products of groups. Moreover, we obtain an algorithm that exactly computes stable torsion length in free products of finite abelian groups. The nature of the algorithm shows that stable torsion length is rational in this case. As applications, we give the first exact computations of stable torsion length for nontrivial examples. (Joint work with Lvzhou Chen.)

Chloe Avery 5/31
Every surface is a leaf

Every closed 3-manifold admits foliations, where the leaves are surfaces. For a given 3-manifold, which surfaces can appear as leaves? Kerékjártó and Richards gave a classification up to homeomorphism of noncompact surfaces, which includes surfaces with infinite genus and infinitely many punctures. In their 1985 paper "Every surface is a leaf", Cantwell–Conlon prove that for every orientable noncompact surface L and every closed 3-manifold M, M has a foliation where L appears as a leaf. We will discuss their paper and construction and the surrounding context.

Recording   Notes
Justin Lanier 5/24
On the Torelli theorems

I will give an overview of the Torelli theorems for curves and K3 surfaces.

Recording
Adán Medrano Martín Del Campo 5/17
Platonic solids and Kleinian singularities

A remarkably long list of mathematical structures can be classified by the simply laced Dynkin diagrams, i.e. those of types A, D and E (but not B or C). I will discuss just some of the connections I’ve learned between different structures sharing these classifications.

Recording
Peter Huxford 5/10
Reflections and indefinite orthogonal groups

Consider the groups O(f, \mathbb{Z}) of integral matrices preserving an integral quadratic form f of signature (n, 1) for some n \geq 2. Such a group is called reflexive if its subgroup generated by reflections has finite index. In 1972, Vinberg proposed an algorithm to determine the reflexivity of these groups and applied it to the case n \leq 17. In this talk, we will give an overview of some basics of reflection groups and Vinberg's algorithm.

Recording
Seraphina Lee 5/3
A strange state of affairs in P^2

We will discuss a combinatorial plane geometry question that is currently best understood using a rather deep result on properties of algebraic surfaces.

Recording
Soohyun Park 4/26
Configuration spaces with summable labels

The nth configuration space of a manifold M can be thought of as the space parameterizing n unlabelled particles in M, such that the particles are not allowed to collide with each other. Configuration spaces with summable labels are variants of configuration spaces where the particles now have names, and there is a prescribed rule for what happens when particles of different types collide (e.g. when a muon and a gluon collide they turn into a pion). Often, important spaces in algebraic topology are secretly configuration spaces with summable labels! I will talk about examples involving classifying spaces and mapping spaces, the Dold-Thom theorem and its generalizations.

Recording   Notes
Phil Tosteson 4/19
A crash course in Tannakian formalism

Just how much information does the representation theory of a group carry about the group itself? Well that depends what you mean by "representation theory" or "group"...

Recording
Nate Harman 4/12

Winter 2021
Title Speaker Date
Quasi-morphism and uniformly perfect groups

What does the Dedekind eta function and the Hirzebruch signature defect have to do with each other? A priori, nothing much. But thanks to the fact that PSL(2,R) and SL(2,R) both act on the circle, the defect of log(eta) and the signature defect of the mapping torus pretty much differ by a constant factor, thanks to a link granted by the Euler class of Homeo^+(S^1).

Recording   Notes
Peng Hui How 3/15
Stable birational equivalence vs. cut and paste relations

We will focus on a result of Larsen--Lunts that gives a close connection between stable birational equivalence classes of smooth projective varieties and cut and paste relations. Following some background and a sketch of a proof, we will give applications to the overall structure of cut and paste relations and specific independence results.

Recording
Soohyun Park 3/8
Finite group actions on 4-manifolds

Suppose a finite, cyclic group G acts on a 4-manifold. What can we say about the fixed set of this action? In this talk, I will discuss some conditions one can impose on the action (e.g. preserving the orientation or the spin structure) and their consequences on the topology of the fixed set.

Recording   Notes
Seraphina Lee 3/1
Polygonal complexes

Polyhedral complexes are 2-dimensional simplicial complexes which are created by gluing together regular Euclidean k-gons along their edges. A natural question is how many (simply connected) polyhedral complexes exist which satisfy some collection of local gluing criteria, up to isomorphism. This talk is an introduction to polyhedral complexes, and gives an overview of some work that has been done in this direction, specifically when the polyhedral complexes are (k,L)-complexes.

Recording
Chloe Avery 2/22
Monodromy of families of hyperelliptic curves

We give a brief overview of the first sections of McMullen's paper Braid Groups and Hodge Theory, exploring unitary representations of the braid group given by the monodromy of a family of hyperelliptic curves.

Recording
Adán Medrano Martin Del Campo 2/15
Line bundles, divisors, and linear systems

We will explore the relationship between some of the fundamental objects of algebraic geometry, divisors and line bundles, from a concrete, geometric perspective, using the language of Čech cohomology.

Recording
Nat Mayer 2/8
Fundamental group of the complement of a plane algebraic curve

To better understand how a variety in affine or projective space "sits" in space, one can try to compute topological invariants of its complement. Such complements sometimes also parametrize the 'nice' or 'smooth' objects in a moduli space. I will discuss a method to compute the fundamental group of the complement of an algebraic curve (over ℂ) in the plane, and explicitly compute some examples. This is based on work originally due to Zariski and Van-Kampen, but the tools used, such as braid monodromy, are also useful in more complicated settings.

Recording
Peter Huxford 2/1
Group cohomology
Ronno Das 1/25
Spectral sequences Recording
Nir Gadish 1/18