A nice day at the pond with my brain and my computer

Posted August 11, 2019

FiveThirtyEight's Riddler Classic this week is a puzzle about crossing a pond on boards. It came from Erich Friedman. Here's the puzzle:

You are the proud owner of a circular pond with a radius of 1 yard. You are also the proud owner of a large collection of thin boards that are each exactly 1 yard long. By placing these boards one by one, so that the ends of each lie on either the banks of the pond or on another previously placed board, how many boards are necessary to cover the center point of the pond with a board?

For example, the solutions for smaller ponds with radii 1/2 yard, 5/8 yard and slightly more than 7/10 yard are shown below:

I was able to do it with 12 boards; I do not know if it's possible to use fewer. Something fun about solving this puzzle was that I used a combination of traditional pencil-and-paper work and computer help, and got a better answer than I could have gotten using only one or the other. I found a systematic way to solve the puzzle with 15 boards, then was able to bring that down to 13. Then, I wrote some code and threw my 13-board solution into it, and the computer spit back out a picture that suggested how to do 12. I describe my solving process below; if you'd just like to see my solution, scroll to the end.

Part 1: Brain

Here is my solution that uses 13 boards:

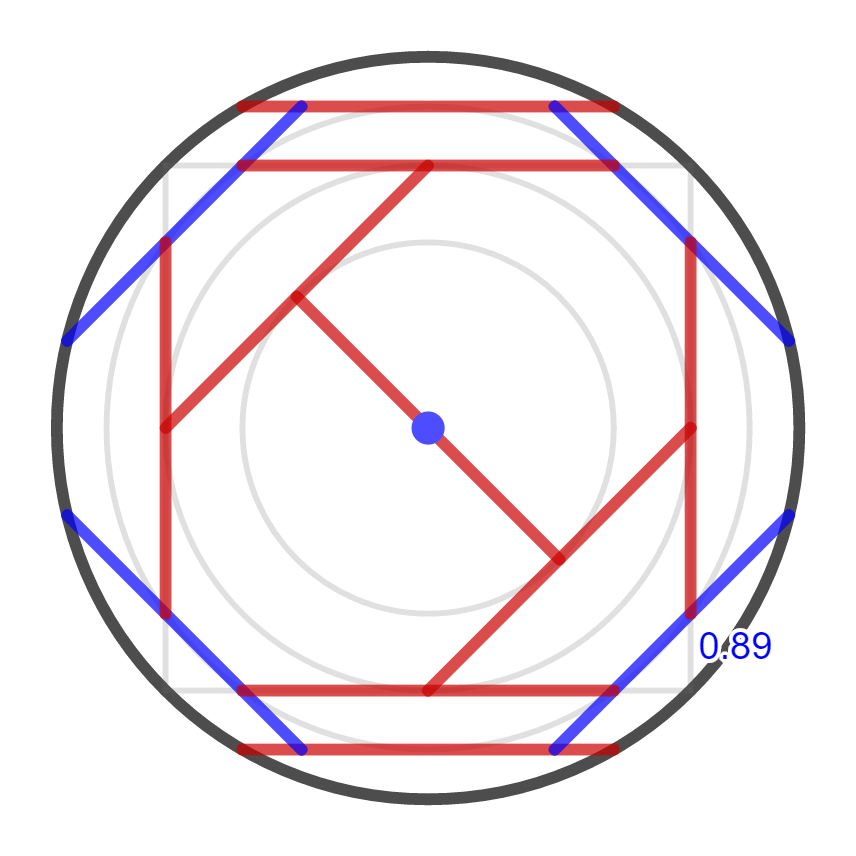
You can see there's some structure to it. All the boards are either exactly vertical, horizontal, or at a 45-degree angle. I've drawn in some extra circles. The circles have radii \(\frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, 1\), which can also be written \(\frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}\). I chose those circles so that a board with both ends on one of the circles has its midpoint on the next-smaller circle, and a board with both ends on the inner circle has its midpoint at the center.

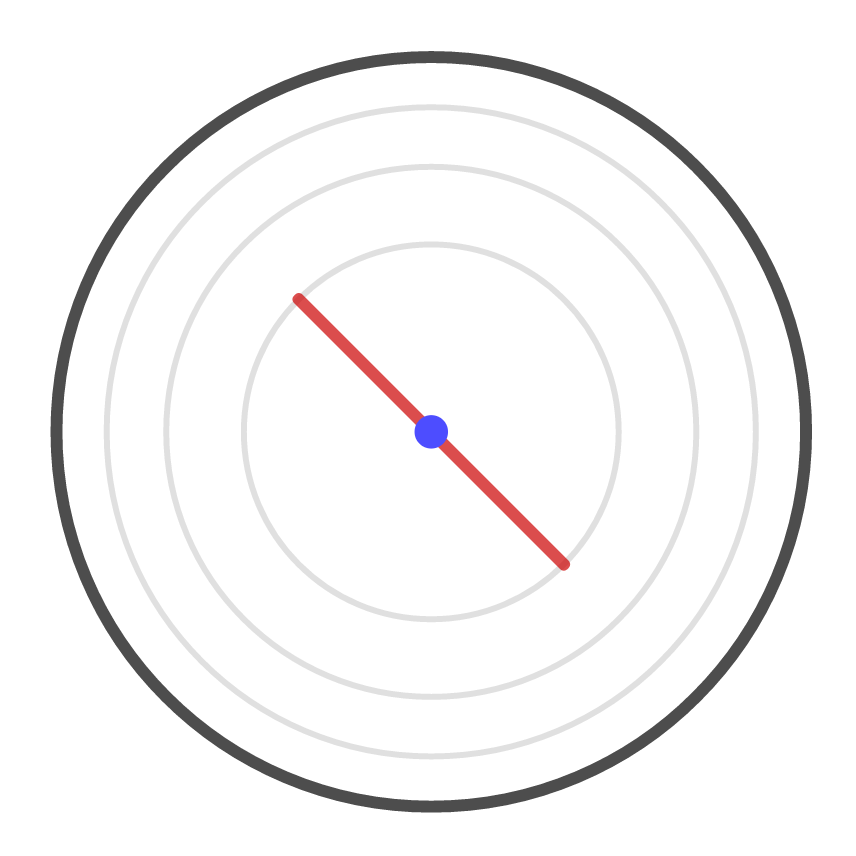
That observation gave a method for building a solution inside-out. Start by placing a board to be the diameter of the innermost circle:

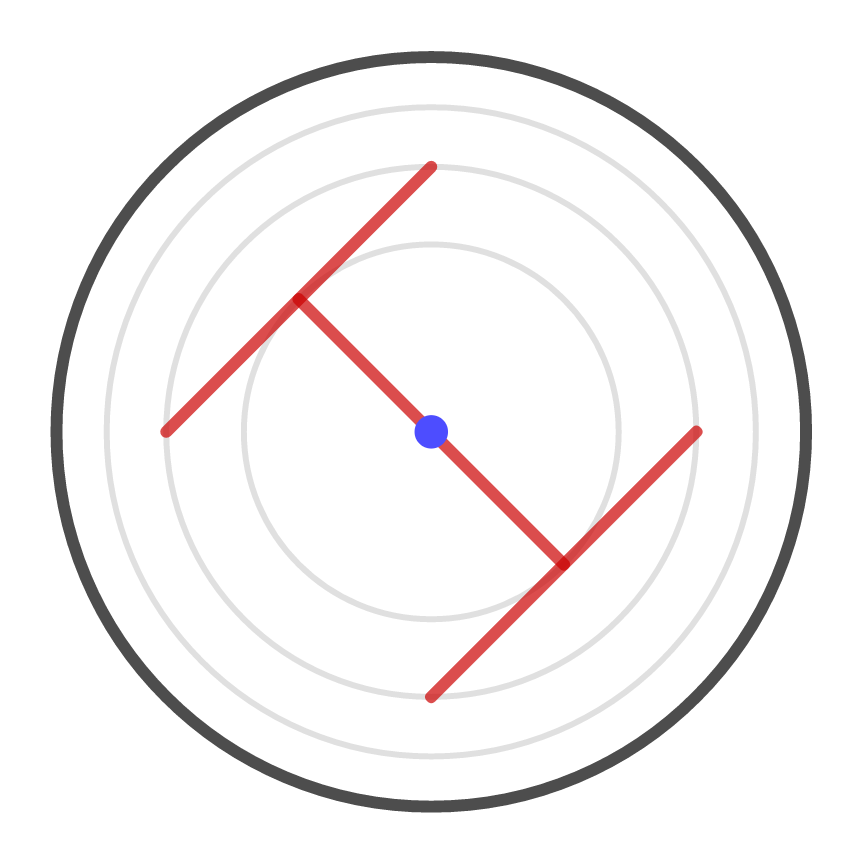
To support each end of this board, place a new board whose endpoints are on the second-from-innermost circle. There are two ends, so this will take two boards:

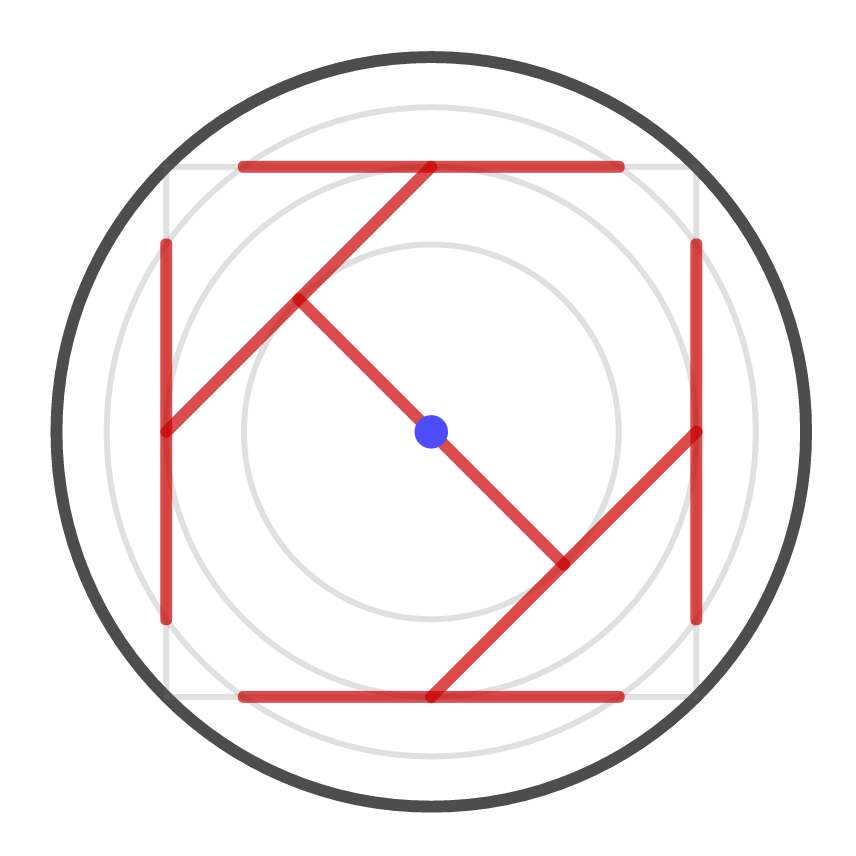
To support one of the ends that is now hanging free on the second-from-innermost circle, place a new board, whose ends are on the third-from-innermost circle. There are currently four ends hanging out, so this takes four boards:

We could repeat this strategy one more time, using eight more boards, though actually it's possible to use just six:

We've used 13 boards in total. Actually, I've cheated a little bit, because four of my boards (indicated in blue) are less than one yard long. But one can prove a general principle that if you can solve the puzzle using \(N\) boards of length at most one yard, then you can solve the puzzle using \(N\) (or fewer) boards of length exactly one yard. There's a general procedure for turning one into the other. Basically, if you are about to place a board of length less than one yard, use a board of length exactly one yard instead. It won't fit in its originally-planned position, but just keep nudging it toward the center of the circle until it fits. The result of applying this procedure to the solution above is the following:

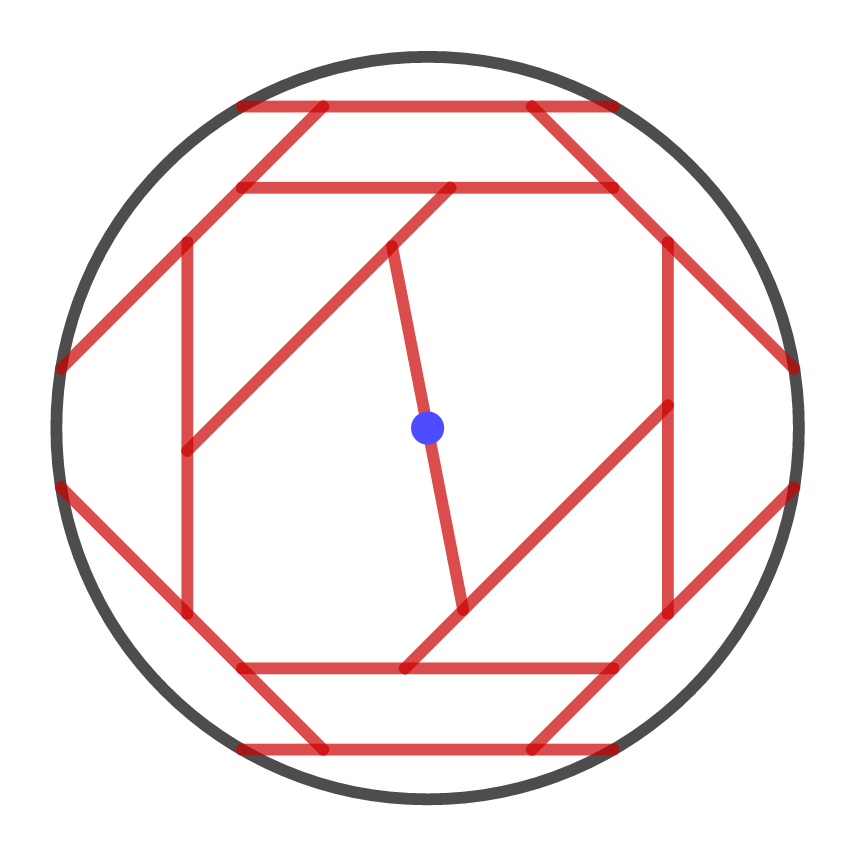
This is a solution that uses 13 boards of length exactly one yard.

Part 2: Computer

As I kept playing around with this problem trying to do better, the numbers got messy fast. It was too much work to figure out the exact best angles to rest the boards on each other. So, I wrote a computer program to do it for me. The way you use the program is that you type in which boards you want to rest on top of which other boards. The computer then tries to find the exact arrangement that gets your final board as close to the center of the circle as possible.

The program was not too hard to write — all the constraints can be represented as polynomial equations or inequalities. For example, here's how to express that the points \(A = (a_1, a_2)\) and \(B = (b_1, b_2)\) are exactly one yard apart: \[ (a_1 - b_1)^2 + (a_2 - b_2)^2 - 1 = 0. \] And here's how to express that the points \(A = (a_1, a_2)\), \(B = (b_1, b_2)\), and \(C = (c_1, c_2)\) lie on the same line: \[ a_1 b_2 + b_1 c_2 + c_1 a_2 - a_1 c_2 - c_1 b_2 - b_1 a_2 = 0. \]

I wrote down the constraints and found a Python library (scipy.optimize) that would do the optimization for me. Problems of this type are called quadratic programs (because they are expressed in terms of quadratic polynomials). There's no efficient way to solve quadratic programs in general. But if you have a small enough instance, you can ask your computer very nicely to solve it, and if you have enough patience you might get back out something useful.

After playing around with my program for a while, and asking it to check through many different configurations, I decided on a whim to try inputting my 13-board solution. I told the computer which boards were supposed to rest on which others, and the computer decided for itself where exactly to place each board. Here's what it came up with:

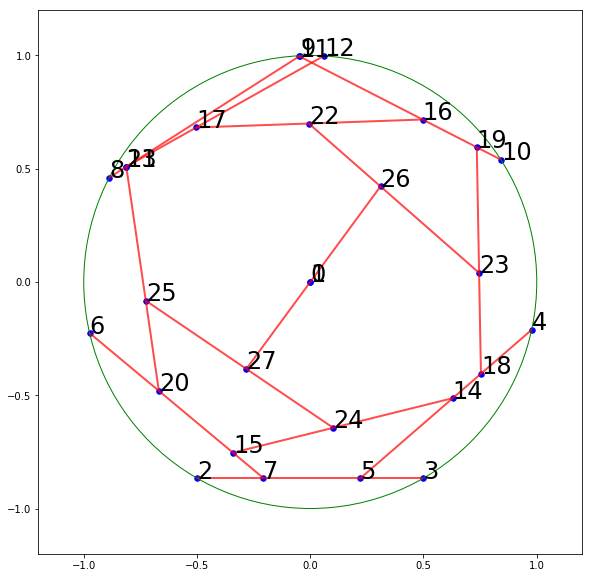
Its arrangement looks like mine, but pushed around a little bit. Surprisingly, it decided to put two of the boards basically right on top of each other. Maybe those two boards could be replaced with just one. When I asked the computer to do that, here's what it gave me:

And that's the best I've been able to do. I don't have a proof that this is the best possible; I'd be interested to see a better solution, or a proof that it's impossible to do better!