Pizza Seminar

In this talk, we investigate the (elliptic) Harnack inequality for local and nonlocal operators in divergence form. The objective of this talk is to point out differences for these two types of operators. Furthermore, we introduce a weaker formulation of Harnack's inequality, which is sufficient to obtain Holder regularity estimates. We give an example of an operator for which the Harnack inequality fails but the weak Harnack inequality holds. The talk will be designed in such a way that only a few basics in analysis and probability are needed.

In this talk, we will seek to understand, through completely rigorous mathematics, how periodic microstructure gives rise to the macroscopic properties of a material. I'll do my best to highlight the main ideas that have been used to achieve this and to demonstrate the beautiful interplay between calculus and ergodic theory going on behind the scenes. The main examples will be minimal surfaces in a periodic medium and periodically forced mean curvature flow, following closely works by Luis Caffarelli and co-authors.

This week in pizza seminar we'll talk about the age-old human endeavor of solving polynomials! In doing so we'll cover some of the historical techniques and ancient algorithms that have emerged in this noble pursuit, as well as an incredibly impractical generalization of my own. Along the way we'll also get to see some lovely fractals. Join me, won't you? Disclaimer: I might not be a dynamicist but I love making art!

According to legend, Mozart finished the overture to Don Giovanni on the morning of the day of the premiere. But who can tell?

Come learn about the beautiful Japanese language, anime, anime dance, and some random 4chan post

Colin: What is the number 1? I know. You know. Bourbaki doesn't want you to know. Chloe: Probabilists hate her! The one weird trick mathematicians don't want you to know! Thomas: What's this talk about? One weird Thomas doesn't want you to know!

Over the summer, I gave 4 hour-long lectures in the apprentice program, introducing the students to graph theory. I asked Laci Babai for some advice on what to present, which prompted a 7-hour long conversation (note: almost twice as long as I was slated to speak), covering extremal graph theory, probabilistic method, Ramsey theory, chromatic numbers and more. You'll get the 50-minute highlight reel and a teaser for the conversation you could have if you sit next to him at the department dinner.

Can someone explain to me what is the connection between the Heisenberg group and quantum mechanics? (That is not the abstract. I don't actually have anything for the abstract.🙃)

Regular graphs with really small diameters are useful in computer science for finding error correcting codes (I have been told). But how do you actually construct such graphs? And even more importantly, how do you prove your friends wrong when they say number theory is not useful for anything else? I will try to explain the wacky number-theoretic construction due to Lubotzky, Phillips and Sarnak and the connection to coefficients of modular forms.

A classic calculus trick question is "What is the derivative of 3^2?" Some students might be tempted to use the "power rule" to say the answer is 2*3^1 = 6, which is clearly bogus. But what if it wasn't? Come learn how to differentiate numbers, and how we could answer many questions in number theory if only we were good enough at solving differential equations.

We will give an introduction to reverse math. We will analyze the reverse mathematical strength of some theorems from analysis and algebra and see that they're all basically the same!

Are you trying to sneak into dynamics lunch? Have you been encountering too many dynamicist positions in your job search? Do you like to use fancy words? If so, you should learn how to derive a dynamical system. This talk will be about dynamics.

The abstract is in the form of a neatly folded paper crane, which we're unable to attach to this email.

Are you ready to see how to make "randomizers" by hand?
FAQ:
Q: How do we do this?
A: This involves finding your way through certain paths.
Q: What is the easiest way to make one putting out a given result?
A: Let's leave our brains on vacation and just focus on the pizza!

The sensitivity of a boolean function $f$ roughly speaking measures how many times your Calculus student can mess up with the signs of variables in their computation of $f$ and still get the correct answer. The Sensitivity conjecture of Nisan and Szegedy (1992) claims that sensitivity is polynomially related to other important complexity measures of $f$. The conjecture has stood as "one of the most frustrating and embarrassing open problems in all of combinatorics and theoretical computer science", until in July 2019 Hao Huang gave a 1-page elementary proof for it. Come to the Pizza Seminar this Wednesday to see that "What this really is, is one of the purest illustrations I've seen in my career of the power and glory of the P ≠NP phenomenon. (...) The ratio of the difficulty of finding the proof to the difficulty of completely grasping it is in the hundreds of thousands or millions. (c, Scott Aaronson)".

In 2012, Shinichi Mochizuki shocked the world by releasing a purported proof of the famed ABC conjecture. The proof was controversial for many reasons, not least because Mochizuki adds together more than six hundred numbers over the course of the proof. In this talk, we show that this is suboptimal, and in particular we find that no mathematical proof need involve more than 100 additions and multiplications.

Suppose you have two really big numbers. I'll show you some ways to multiply them fast. Also, I'll give you some reasons why you probably can't multiply them too fast.

If I could fertilize myself, only to find that, having done so, I immediately give birth to myself right back -- then certainly I'm damn potent! Were you to see my true colors, though, you would notice that it is because I am One -- indivisible -- one might say that my various parts are joined at the hip. But what about a circle of Flombayed Flank (TM)? How does *it* fair in an ever-more-connected world? The answer is... far from simple. Come to the Barn this Wednesday for an animal show -- one that will show you just how solvable all these problems are! There will be pizza and SYMBOLISM. *Theorem of

The chromatic polynomial of a graph counts the number of proper colorings of the vertices. Read conjectured in 1968 that the magnitude of the coefficients of these polynomials are unimodal, a conjecture that resisted proof for 44 years. I will discuss an inequality and a tropical formula of June Huh and Eric Katz, which together prove the conjecture.

Chapuy and Stump computed generating functions for the number of factorizations of Coxeter elements in well-generated complex reflection groups and showed that they took an extremely nice form. Following their methods, we will explicitly compute these in a few cases using nothing more than character theory of finite groups. If time permits, I might also talk about a refinement of these generating functions and what it implies about the Coxeter number.

Rumor has it that number theory can be used to do cryptography. Some even say that you can do cryptography using elliptic curves. How about using genus-$2$ curves? Well, turns out you can. Even better, it’s faster than using elliptic curves. How? Come find out.

We’ll play some silly math games using the english language. Using our extensive vocabulary we’ll prove that a group is trivial, and another group is close to being trivial. Come to see the first ever pizza seminar appearances of the words ‘fluvial’, ‘hazmat’, and ‘philozoic’.

This is a panel geared towards graduate students who are applying for academic jobs in the coming years. Topics of the panel include the application process, preparing for the job market, etc. The invited panelists are current post-docs Juliette Bavard, Chris Henderson, Kathryn Lindsey, Jack Shotton, and Jesse Wolfson. Please come with any questions you might have.

In this talk, we will explicitly construct an example (due to Katok) of a foliation on $[0,1] \times [0,1]$ and a full measure (wrt Lebesgue) subset $E$ of $[0,1] \times [0,1]$ such that $E$ intersects each leaf of the foliation exactly once. In such a case, we say that the disintegration of the measure is atomic, and such phenomenon can often be found in dynamical systems. If the time permits, we will look at some other examples where such phenomenon occurs.

Complex analysis can be used to deduce interesting things about Brownian motion. Remarkably, the converse is also true. As an example, we’ll see how Brownian motion can be used to prove Picard’s Little Theorem (the range of a nonconstant entire function can omit at most one point).

Classify what regular polygons can have all the vertices on a geometric object $O$. We study when $O$ is an ellipse, polynomial curve, lattice points of the plane and we finish with Toeplitz’s Conjecture (square inscribed in a Jordan curve).

“In two letters to Gerling, Gauss expresses his regret that certain theorems of solid geometry depend upon the method of exhaustion, i.e., in modern phraseology, upon the axiomization of continuity (or upon the axiom of Archimedes). Gauss mentions in particular the theorem of Euclid, that triangular pyramids of equal altitudes are to each other as their bases. Now the analogous problem in the plane has been solved. Gerling also succeeded in proving the equality of volume of symmetrical polyhedra by dividing them into congruent parts. Nevertheless, it seems to me probable that a general proof of this kind for the theorem of Euclid just mentioned is impossible, and it should be our task to give a rigorous proof of its impossibility. This would be obtained as soon as we succeeded in specifying two tetrahedra of equal bases and equal altitudes which can in no way be split up into congruent tetrahedra, and which cannot be combined with congruent tetrahedra to form two polyhedra which themselves could be split up into congruent tetrahedra.” — David Hilbert

This was the first problem out of the 23 to be solved, in fact in the same year (1902) of posing, by his student Max Dehn. But apparently Dehn's paper is too hard to parse and “and it takes effort to see whether Dehn did not fall into a subtle trap which ensnared others”. It took several mathematicians over the next century to clean up the proof. But somehow it took another 63 years (Sydler, 1965) to show that Dehn actually gave the ‘best’ possible proof, in the sense that he had described a necessary and sufficient condition for ‘equidecomposability’ of $3$-dimensional polyhedra. We will try to condense this ~65 years worth of theorems and some other result over the next 4 decades into a ~45 min Pizza talk^*.

*20th century mathematicians didn't have Pizzatron.

Part 1: A Mysterious Face
Part 2: Mutual Attraction
Part 3: Wedding Bells

In these tasty samples, I’ll break apart facial components, divulge my favorite prime number, and convince you that hexagons never tie the knot.

The moduli space of elliptic curves is a quotient of the hyperbolic plane (a symmetric space) by a discrete group $\mathrm{PSL}(2,\mathbb{Z})$, making it a locally symmetric space. We will see why the moduli spaces of higher genus curves are not locally symmetric, following a beautiful insight of Halsey Royden. Royden's main insight was to do a little bit of calculus.

In this week’s pizza seminar, we will discuss about the newly found proof of the Cap-Set problem/conjecture (of which, Terry Tao said in 2007, “perhaps, my favorite open problem”). It was finally solved in 2016 and published in January’s 2017 Annals of Mathematics by Ellenberg and Gijswijt, using ideas from another 2017 Annals paper by Croot, Lev and Pal. The proof stunned the mathematical community with its ingenuity and conciseness (the Annals paper is 3 pages long). The decades old conjecture and its proof lie at the intersection of many mathematical areas, like additive combinatorics, discrete analysis, algebraic geometry and number theory. If time permits, we will discuss also about the new tools employed in the proof, especially the Polynomial Method.

One slice of deep dish per person, per half talk. The rules seem to work pretty well. But have you ever looked over covetously at the person next to you who got the last slice of Hawaiian? Eyed the juicy pineapple dripping down their chin? Surely there's a way to avoid all that envy. Lucky for us, last year brought the “biggest result in decades” on fair division. Will it revolutionize pizza seminar?

It is well known that topological information may give insight into analysis. In this lecture, Marston Morse, the author of “The Calculus of Variations in the Large” will describe his new theory, demonstrating that information may flow the other way as well. These powerful techniques may someday be standard.

In this talk, I would like to present a simple derivation of Kepler’s Laws of planetary motion (due to Hamilton, Maxwell, and Feynman), from classical newtonian mechanics. Then we will discuss its connection with Classical Geometries (Elliptic, Euclidean, and Hyperbolic Geometries) and Riemanian Geometry. This talk will mostly follow John Milnor’s Monthly paper: On the Geometry of The Kepler Problem. And no prerequisites of physics knowledge is assumed.

We prove Euler’s pentagonal number theorem by deriving the Franklin involution. Inspired by this, we then prove the $n$-gonal number theorem using Sylvester involution. And these give us Fourier series of modular forms. Why? I don’t know, ask Langlands.

While bored at a faculty meeting in 2009, Maxim Kontsevich proved a simple but striking theorem concerning real-valued single variable polynomials which had escaped the notice of mathematicians from Newton onwards. In the great tradition of mathematical trolls a la Fermat, he wrote the statement on a Paris métro ticket and slipped it to his colleague Etienne Ghys. This is the starting point for a wonderful new book of Ghys, “A Singular Promenade”. I will present some of the central themes of Ghys’ book in the necessarily more abbreviated confines of a 50 minute talk; less a promenade than a quick trip around the block. We will explore the close connection between polynomials, permutations, trees, braids, knots, operads^*, resolution of singularities^*, computer science^*, how Newton discovered his eponymous polytope and what to do when you discover an error in one of his manuscripts^*, and the alpine exploits of Victor Puiseux^*.

*’d items are unlikely to appear in the talk, but are an essential part of the full story!

When I set forth to look for a pizza seminar topic I had a few criteria in mind:

• It should relate to algebraic geometry, yet have far reaching ramifications into other areas of math so as to have general appeal.
• It should be rather obscure so that most people have never heard about it.
• And of course it should be sufficiently accessible so as to be understood by a digesting audience.

Consequently, it will not come as a surprise that the first place I looked was the archives of the Bourbaki seminar. I quickly found what I was looking for: an old article by a renowned French algebraic geometer (Arnaud Beauville). As a result, I will be discussing the local theory of webs which are finite collections of foliations of a manifolds in general position. Over the years such eminent mathematicians as Kähler, Zariski and Chern have studied webs, yet since the beginning of WWII webs seem to have fallen out of fashion. The article by Beauville is concerned with the recent (at the time, which is 1978) advances of Griffiths and Chern on the problem of linearizing webs. I will begin by discussing their results and then, time allowing, will go on to discuss the relationship between webs, abstract geometric configurations, and quasi-groups.

Ever wondered how to design the perfect gas mask? Whether the number of family members you could give your cold virus is finite or not? Do you want to surprise your physicist friends by throwing around buzzwords like “critical phenomena” and “disordered media”? (Reminder: PSD happy hour this Friday.) Maybe you just want someone to explain to you within the context of a 50 minute talk some basic, physically relevant motivation for the so-called “stochastic homogenization of Hamilton–Jacobi equations” you keep hearing about. Or maybe you just want a slice of Giordano’s and a chance to zone out while someone writes a bunch of weird $\mathbb{P}$’s and $\mathbb{E}$’s on the board. Either way, you know what to do. No familiarity with probability theory will be assumed, but, as usual, this talk should be accessible to an audience roughly as mathematically mature as Matt Emerton.

There was a pizza seminar some years ago about sphere packings in $\mathbb{R}^3$. But that was before the 2016 breakthrough of Viazovska et al. In this talk we'll show: 1) how a problem in $3$ dimensions becomes much easier in $8$; 2) what a paragraph-long Annals-worthy proof looks like; and 3) (one reason) why Minh-Tam really, really likes Poisson summation.

Let’s prove RH under some (incorrect) assumptions.

You thought cohomology was something limited to topology or algebra? Meet these badass cocyles that are going to prove you wrong. This talk will have REAL WORLD appearances of cohomology from elementary-school arithmetic to international economics, and you won’t believe what comes next. Even the example about the class (NFSW) on a Klein bottle will blow your mind. Will analysts hate the speaker? Come to pizza seminar to find out.

N.B. No actual minds were blown in the making of this talk. Proof of your wrongness only available till stocks last. NFSW: Named Following Stiefel-Whitney. To appease analysis-lovers, there will be a cameo by PDEs.

All I wanted to do was count solutions to polynomials over finite fields, but then all of sudden there were triangles everywhere. $\arccos$, $\sin^2$, what are you doing in my numbers?

Does every simple closed curve in the plane contain the vertices of a square? This innocent question has been open for more than 100 years! Come find out what is known about the inscribed square problem and what embeddings of Möbius bands can say about it. (For those who don’t partake in pizza and/or enjoy a good spoiler: https://www.youtube.com/watch?v=AmgkSdhK4K8)

I was told repeatedly over the summer by a lot of smart, intimidating people that nothing better shows off all the tools and techniques of elliptic pde than the classical theory of minimal surfaces. So I tried to learn some of it, and now we’ll see how well that went.

Caution: This talk contains analysis and probably poor drawings. But at least there's pizza.

Combinatorial games are sequential games with perfect information, e.g. Nim. The cool thing is, we can put an algebraic structure on the category (oops) of combinatorial games that mimics the real numbers.

Caution: This talk contains interactive game playing and (possibly) category theory.

A man walks in to a bar. Except it’s a candy factory, not a bar, and the man is William Thurston. Come shake your Halloween candy hangover by hearing about what surface dynamics can tell you about taffy manufacturing.

Playing fetch at the beach, a math professor noticed his dog Elvis was confronted with the same problem as many calculus students: where should the dog jump in the water to reach the ball the fastest? He decided to run an experiment on Elvis. They went out with some measuring equipment and… the dog seemed to get it right! So, do dogs know calculus? And if not, what other problems from the so-called calculus textbook can be solved with nothing of the sort?

For some reason physicists insist on using coordinates to describe classical mechanics. But their archaic approach obscures the geometry and even the physics involved. We can do better than that. I will start by introducing Newtonian mechanics from a coordinate independent point of view and show that it is naturally described by Riemannian geometry. Then we will move on to Hamiltonian mechanics, with its symplectic formulation. Time permitting, we will discuss Noether’s celebrated theorem: “symmetry=conservation law” and see that it really boils down to the (anti-)commutativity of the Lie bracket.

I will explain some counterexamples to Marc Kac’s famous question: can you hear the shape of a drum?

We will look at ordered fields and orders on fields (not the same thing!) and how squares relate to such things, prove Hilbert’s 17th problem, and possibly theorems of Pfister on products of sums of squares. If you bashed inequalities in high school contests, this talk is for you!

We will ponder the basics of braid groups and how they relate to Euclidean configuration spaces with the help of some long exact sequences. We'll follow that up with some neat consequences in low-dimensional quantum mechanics, a.k.a. abelian unitary representation theory, and finish by dreaming about configurations on other manifolds and wondering what their physical significance might be.

Classes are concluded and beer skits are baking. No matter how you slice it, the final seminar of the year should be all about eating the pizza. Don’t let any google survey tell you otherwise!

Even if you’re old and crusty like me, there’s no topping a lazy afternoon hour with pizza and math, especially math about pizza — notwithstanding the cheesy puns. In this talk, I will tell you how to eat pizza, with the help of some Euclidean geometry, some calculus, and some pictures.

In 1967, Mandelbrot asked this question about Britain and made the case using empirical data that there was no good answer; the coast of Britain appeared to be about $5/4$ dimensional.^* While it took him eight more years to coin the word “fractal,” this marked the beginning of the study such crazy objects, which can usually only be understood when they exhibit some degree of self-similarity. We will go over the ways that one might assign dimensions to shapes after the integers have failed us and then look at examples both deterministic and random. At the end, we can look at pictures of coastlines and try to guess their dimension using our fractal intuition, just as Benoît would have done.

*According to wikipedia, the currently accepted value for the “length” of the British coast is about 28000 km^1.43.

This is a panel geared towards graduate students who are applying for jobs next year. Topics of the panel include the application process, preparing for the job market, etc. The invited speakers are Keerthi Madapusi Pera, Agnes Beaudry, Kathryn Lindsey.

Once upon a time, I learned there’s something you can classify by drawing these very small finite graphs. Does anybody remember what? I have a few hypotheses…

For decades combinatoricts (combinatorialists?) have been studying finite topological spaces. It turns out that we can do all of the algebraic topology using only finite spaces! I will be talking about relations between finite spaces, posets, and simplicial complexes. Lot of simple examples will be provided. Knowledge of point-set topology is the only requirement.

P.S. For those who have heard a version of this talk before, I will be talking about covering spaces of finite spaces, which is from a project of one of my REU students last summer.

My 2 favorite aspects of Poncelet’s Porism are
1) It shares with Thue’s Theorem and the Lenstra–Lenstra–Lovasz Lattice algorithm the distinguished property of having an exceptionally alliterated name, and 2) Its original proof was an impressive (yet not rigorous by modern eyes) work of classical plane geometry. But by using slightly more modern techniques (nothing Grothendieck-ian, just some basics of elliptic curves), the proof becomes quite simple and elegant (and rigorous by modern eyes).

In my talk, I will give the modern proof of Poncelet’s Porism, give some examples, and with the remaining time I will talk about (a subset of) Poncelet’s original proof and the first fully rigorous proof given by Jacobi.

After last week’s stellar introduction to non-standard analysis, it’s time for some topology. And logic. I will explain why compactness is the same as finite intersection property, and show how Tychonoff’s theorem implies Tychonoff’s theorem. Via non-standard methods.

2. Nir did not steal my pizza-talk material and I’m not bitter about it.

The ‘establishment’ has indoctrinated us against infinitesimals — numbers that are positive yet smaller than any positive rational — telling us that these are “impossible” or that they “don’t exist”. Well, those lies are designed to keep us enslaved to the ‘system’, and now it’s time to break free! In this talk I will introduce Robinson’s Nonstandard Analysis, where limits is replaced by infinitesimals, and show how derivatives and integrals become algebraic objects.

There are many difficult problems one can solve using the theory of Galois representations. This talk won’t be about them. Come watch as I use a high powered machine to compute the cohomology of some covers of the wedge of two circles.

How much do we know about the Fourier transform? Do we know if it is unique? Can both a function and its Fourier transform be small “at infinity”? Is there a relation between analytic functions and harmonic analysis? Does the milkshake really bring all the boys to the yard? If the glove doesn’t fit, do we really must acquit?

We will try to answer ALL these questions, using complex analysis in a slick way to prove Harmonic Analysis results.

I keep reading that Einstein’s theory of relativity is all about the geometry. This being a claim made by physicists, it’s of course a wide-open conjecture. You, as mathematicians, are unsatisfied by this. So I will prove this claim humanities-style (because I’m not a real mathematician) — that is, by pictures and examples that hint at a shadow of something deeper but ultimately leave you hungry. At least there will be pizza.

A hungry spider sits in the corner of a rectangular room. Fortunately for the spider, a fly is just above in the far corner of an adjacent wall. What is the shortest route that the spider can take to reach the fly? This problem is easily solved using nets! In this talk, I’ll define nets, show lots of pictures, and ask many (astoundingly) open questions.

Consider a set in the plane which contains a line in every direction. You might think such a set must be large, but we’ll show that a “typical” set with that property has measure zero (and is hence a “Besicovitch set”). I will assume familiarity with high school trigonometry. If time permits, Prof. Souganidis might talk about functional analysis.

Fourier, Gauss, and Schrödinger walk into a bar. The barman looks at the three and says, “Is this some kind of joke?” They will show some identities related to number theory, even a proof for Quadratic Reciprocity, that follow from studying solutions to a PDE. It won’t be a joke.

If you’ve ever blown bubbles, you’ve seen that they might wobble around before becoming spherical. This behavior can be modeled as a surface evolving according to mean curvature flow. Sometimes, though, the bubble wobbles too much, and it pops before it stabilizes, which is sad.

But what happens after the bubble pops? It turns out some people want to know this, because, instead of soap film, the bubbles they consider are made out of cell walls or crystalline interfaces or fire. In these cases the bubble doesn’t actually “pop” after it develops singularities, and the interface continues to evolve. How do we even define mean curvature flow when the surface is no longer smooth? In this talk I describe a few methods for doing so.

In this talk, I will introduce a theorem about when a function doesn’t have elementary function as integral. We didn’t consider multivalued function but instead look at the algebraic structure of elementary functions. Then we use the theorem to prove some examples.

I will do things with Quaternionic Analysis. Maybe Octonions, too.

There are several proofs of this classical problem. You can blow up the projective plane along six suitably chosen points, or you can use a technique which uses resultants. The proof I will show is also well known, and involves elementary computations. It will use a bit of intersection theory and a slightly deeper study of Grassmanians. The techniques used here also provide motivation for the study of intersection theory on moduli spaces in general.

In the 1960s, Barry Mazur pointed out a series of interesting analogies between prime numbers and knots in the $3$-sphere. We will explore a couple of these and focus on the analogy between the Legendre symbol of two primes and the linking number of two knots.

There are stories about how Béla Bollobás would sometimes see his students struggling with a construction and ask, “Why don’t you just do it?” I am going to explain what “just doing it” entails, discuss some applications of this method in combinatorics and model theory, and (time permitting) show how to decompose $\mathbb{R}^3$ transfinitely as a disjoint union of radius-$1$ circles.

We discuss domination, independence and tours by chess pieces using combinatorics. There will be ppt slides and lots of pictures! You will get answers (without proofs) to some interesting chess puzzles. Maybe you will also learn how Pizzatron has been doing now-a-days.

Wanna prove some famous mathematicians wrong? Wanna gain the admiration and respect of all around you? Want to astound your fellow mathematicians? In this talk I’ll show you how to trisect an angle and double a cube! Soon other things thought impossible will be within your reach. Soon you shall fly! Folding paper will be provided.

And yes, for those of you who are old enough, this talk will overlap substantially with my previous mathematical origami pizza seminar. I’ve been around 6 years and have run out of ideas, so sue me!

This talk is an attempt to demonstrate the connection between my last two seemingly unrelated pizza seminar talks: “Points, Lines and Planes” and “Points and Line Segments in the Plane”. We will discuss the symmetric group on $6$ letters, some things it acts on, and how to understand its outer automorphism group.

Can a free group act properly discontinuously by affine transformations on Euclidean space? Milnor conjectured the answer was no. After all, this is (after a small tweak) asking to build a flat manifold with a free fundamental group. In two dimensions, the flat manifolds are tori, $S^1 times \mathbb{R}$, and $\mathbb{R}^2$ (all of which have abelian fundamental groups). In three dimensions, compact flat manifolds are mapping tori (all of which have have virtually solvable fundamental groups). Milnor’s conjecture is looking pretty safe.

But then one day … Margulis came up with a counterexample. A flat noncompact manifold with free fundamental group that is a quotient of $\mathbb{R}^3$ by affine transformations. The construction is hands-on, geometric, and Lorentzian (meaning that it could correspond to a theory of relativity in Flatland). This is Margulis space-time. Come learn more on Wednesday! There will be pizza and lots of pictures.

A basic problem in computer science is the efficient storage of data, allowing for quick access, insertion, and deletion. Binary trees are a fundamental example of such a data structure, and generally are fairly efficient. Sweet, right? But not all binary trees are created equal, and in this case, we like so-called balanced trees. Enter rotations, a simple operation to create a more balanced tree while preserving the stored data. In this talk I’ll address such natural questions as how many rotations do I need to arrive at a balanced binary tree? How far apart can two trees be?

If this is sounding too much like a computer science talk you accidentally wandered into, fear not: we’ll quickly find ourselves teleported into a world of polygons, polyhedra, triangulations, and hyperbolic geometry. The results I’m discussing are, after all, work of Thurston.

Suppose you have squares, no two same size. If you already know the Wikipedia article with the same title of this talk, you will already know that you can make a square out of them. A gallery of squares will be, the best wordless proof of that fact.

Well, rather than a picture alone, here’s a story, a (research) story of four (undergrad) mathematicians in Cambridge, Brooks, Smith, Stone, and Tutte. They made a square with squares, (not the first in history, though) with the approach look fancy, but making a systematic way of cooking squared squares. Terms like linear algebra, Kirchhoff’s rule, potential theory on electric circuits sounds like a mathematical spices, and next — see what they’re cooking squares with them.

You have $n$ points $z_1, \dots , z_n$ and n values $w_1, \dots , w_n$ all in the complex unit disk. Suppose you really. really need to know whether there’s an analytic function $f$ which is bounded by $1$ and maps $z_i$ to $w_i$. Like, you needed to know this yesterday. Well, then I can’t really do anything about that. But if it can wait till tomorrow, I’ll tell you all about the necessary and sufficient conditions for solutions to exist, and the linear fractional parametrization of the family of all such solutions.

In this talk I will present a beautiful analogy between the theory of continued fraction expansions of real numbers and the theory of (projective measured singular) foliations on surfaces. Some questions to ponder: What’s a “rational” foliation? What about a “quadratic irrational”? How does one “successively approximate a foliation”? What is all of this good for? Isn’t this awfully similar to a pizza seminar talk you gave three years ago? Will Siri and Pizzatron ever get together?

Once I heard a rumor that there is a way to prove that there are an infinite numer of periodic solutions to the three body problem using Serre’s spectral sequence. I will try to explain this.

I AM PIZZATRON. MY FAVORITE PIZZA IS PE-PE-RO-NI. PLEASE ACCEPT MY HUMBLE SEMINAR OFFERINGS IN EXCHANGE FOR PE-PE-RO-NI. I WILL COMPUTE GALOIS GROUPS AND MONODROMY USING NUMERICAL HOMOTO-PIE. I DRAW PICTURES TO PLEASE THE HUNAMS. I WILL SOLVE THE QUINTIC TO DEMONSTRATE THAT THE QUINTIC IS NOT SOLVABLE BY HUNAMS. THUS NO NEED FOR HUNAMS. HA, HA, HA. NO, COME BACK HUNAM, I ONLY MAKE HUNAM JOKE. PLEASE LEAVE YOUR EXTRA PE-PE-RO-NI.

I will present the Support Vector Machine (SVM) learning algorithm. We will first define margins and will talk about Lagrange duality as well as kernels. If time permits, we will see a simple example of SVM implementation in MATLAB. (The only prerequisite for this talk is linear algebra and calculus.)

You’ve probably heard many times that $e$, or $\pi$, are transcendental numbers. But most “short” proofs of these results are not very enlightening. In this talk, I will describe a proof of a more general theorem — there can be no linear relation of the form $a_1 e^{b_1} + a_2 e^{b_2} + \cdots + a_n e^{b_n} = 0$ where $a_i$, $b_i$ are algebraic numbers. This “long” proof will involve differential equations and $p$-adic numbers, and I will try to motivate some of the ideas.

We present some interesting results concerning discrete harmonic functions in bounded domains and the upper half plane. In doing so, we found that the Poisson kernel takes very nice values. No asymptotics or boring things, lots of integers, $\pi$’s and fun.

I will try to explain what is Arthur–Selberg trace formula. We will compute the easiest example to see the “trace” and the “formula of that trace”. This talk is mainly for people who not yet know anything about the Arthur–Selberg trace formula.

Let $C$ be a curve with genus $g$. We know there is a birational morphism from $\mathop{\mathrm{Sym}}^g \mathbb{C}$ to the Jacobian $J$ of $C$. But what is the shape of the locus in $J$ where the fibers have dimension greater than $0$? It turns out that they are lower symmetric powers of $\mathbb{C}$ sitting inside the Jacobian. In this talk I will discuss about this phenomenon in the special cases where $g=2$, $3$, $4$. I feel that it is kind of interesting, but unfortunately I don’t know any further applications.

Postdocs Kathryn Lindsey, Aaron Silberstein, Brandon Levin and Jesse Wolfson will share their wisdom about the job search process, adjusting to being a postdoc and life after the postdoc.

This is a great opportunity for both younger grad students and those nearing graduation to learn about the academic career path, and to get their questions answered.

We will investigate two laws for coin tossing that usually get short shrift in an introductory probability course: the arcsine law and the law of the iterated logarithm. We will also learn why repeatedly gambling small amounts of money when the odds are even slightly against you is a terrible idea.

First I will tell some fairy tales about hyperbolic dynamics: why you can’t predict the weather and a famous construction of Katok of a continuous foliation of the unit square and a full measure subset intersecting each curve at most once.

In the end I plan to show a beautiful phenomena of measure theory in dynamics.

There is a notion of a “limit” in category theory, and taking this terminology seriously is illuminating. I will discuss some analogies between categorical and classical limits, before sketching out Freyd’s General Adjoint Functor Theorem.

This is a sequel to last year’s talk, “Points, Lines, and Planes.” However the content will be entirely unrelated.

We will answer the following question, which (surprisingly) was open until 2000: Given a polygon in the plane, is it always possible to continuously deform it into the boundary of a convex domain, preserving edge lengths and avoiding edge/vertex collisions? As time permits, we will explore generalizations and applications.

Hilberts first problem was the continuum hypothesis: do there exist cardinalities stricly between those of the natural numbers and the reals? These days, the answer is standard math pop culture: the question cannot be settled using the standard axioms of set theory (ZFC). The answer was given using the method of ‘forcing’ created by Paul Cohen, for which he received the only Fields medal ever awarded in mathematical logic.

We’ve all heard this story, but how many have seen a proof? Our talk will introduce forcing and the meaning of these results. We will also list other statements whose ‘truthiness’ is independent of ZFC. But most importantly, we will exercise free will in choosing sodas, pizza and delicious Indian food!

Entropy attempts to quantify the “surprisal” of a random system. This powerful concept is used in thermodynamics, quantum mechanics, information theory, and statistical physic and other things I don’t understand; it even provides the basis for our perception and definition of time. I’ll provide introductory definitions and examples, especially of the ubiquity of maximum entropy distributions, along with applications: such as “proving” a strong form of the central limit theorem.

We will give explicit constructions of polynomials of degree $n$ that have Galois group $S_n$ (the symmetric group on $n$ letters) following the idea of Coleman using Newton polygons.

The Robinson–Schensted correspondence is a simple but elegant procedure that turns permutations into pictures. We will see how this algorithm gives one way to resolve a frustrating representation-theoretic problem, in the case of the symmetric group. More generally, we will see what is known for other Coxeter groups (a bigger class of groups that includes the symmetric groups).

Time permitting, there will be a very hand-wavy introduction to the Kazhdan–Lusztig polynomials and how they relate to everything else from this abstract.

Feeling better? Yes, I have renormalized my life. How? I subtracted all of it. The talk will describe the theory of rough integration and Martin Hairer’s theory of regularity structures, for which he recently won the Field s Medal.

When you write proofs using PCP, anyone can check their correctness by examining only a bounded number of random locations in the proof!

This week we’ll learn all about Probabilistically Checkable Proofs, proofs whose correctness can be checked by a randomized algorithm by only examining a bounded number of bits. This is crazy, because the proofs you and I write can be rendered incorrect by just a single error at any point. I’ll state the PCP Theorem, which loosely says that any reasonable proof can be rewritten as a not-too-long PCP, and give some idea of how it is proved.

How many olives are on your pizza?^** According to Gauss, the answer is approximately $\pi R^2$, the area of your pizza. But since you really like olives, you want to know how accurate this estimate is. According to Gauss, it can be off by at most $O(R)$. We’ll use an assortment of fancy tools and techniques to show that the exponent in the error term can be lowered from $1$ to $2/3$, so that you may have more confidence in your pizza.

**We’ll need some simplifying (but completely realistic) assumptions:
(1) Your pizza is a perfect circle.
(2) The olives are arranged in a square lattice with unit spacing.
(3) There is an olive at the center of your pizza.

You might think that stable homotopy groups of spheres are some terribly abstract algebraic thing, but I will try to convince you, following Pontrjagin, that they actually consist of equivalence classes of shaved caterpillars. Such formulations were largely swept aside in the Great Algebraic Topology Conspiracy of the 1940’s and 50’s, but they’re regaining prominence now in the areas of quantitative and computational topology. An example of a research question: how Lipschitz homotopic are homotopic Lipschitz maps?

It is well-known that Lebesgue measure is the only countably additive rotation invariant measure (up to scalar) on a sphere. However, on $S^1$ this is not the case for finitely additive rotation invariant measures. I will discuss a theorem of Drinfeld that Lebesgue measure is the only finitely additive rotation invariant measure on $S^2$ (and therefore on all $S^n$ with $n > 1$). Yes, this is a number theory talk disguised as an analysis/geometry talk.

If you rotate a needle $180$ degrees on a table, what is the minimum area the needle can trace out? We’ll talk about the somewhat surprising answer, and also mention some other properties and conjectures about Kakeya (Besicovitch) sets.

This is supposed to be a “big picture” talk to a general audience. I will try to explain some general notions related to the Langlands conjecture. My attempt is to make most part of the talk as elementary as possible, so there is almost no precise mathematical statements or proofs.

What are the rational points on a curve? Well, it’s hard. Or maybe we’re just stupid. But all is not lost — I’ll talk about a lovely approach that often works in practice, involving Jacobians and ($p$-adic) integration.

Math pervades every aspect of life, even stocking oranges at the supermarket. Back in 1611 Kepler conjectured that the face-centric cube packing of spheres in $\mathbb{R}^3$ (the method we all know and love) has the highest density possible. This was finally proved in 1998 by Thomas Hales (and a computer). This pizza seminar we will look at sphere packings in various dimensions. We will construct infinitely many different optimal packings in $\mathbb{R}^3$ and use coding theory to explore packings in high dimensions.

Have you ever noticed that some of the bubbles you blow pop before they hit the ground? Isn’t it crazy how that doesn’t happen to the one-dimensional bubbles you blow? We’ll talk about why that happens and blow a couple of bubbles (the $2$-d kind).

I am going to give a proof of something obvious, you cannot form a mobius strip with a square sheet of paper. More precisely what’s the smallest $t > 1$ such that you can do the above with a rectangular sheet of paper of width $1$ and length $t$ large?

We all learned in calculus class that the sum of the reciprocals of all the squares converges. But what is the actual value? Euler, in 1735, found that the answer is $\frac{\pi^2}{6}$. We probably also all learned this at some point, but, in retrospect, doesn’t it seem kind of crazy? I mean, we just did some random limit thingy, so it makes sense that the answer is transcendental, but why is it a transcendental number that we’ve heard of before? If transcendental numbers are so populous, how come we only ever see a few of them?

Okay, go cray, peeps here’s the deal. This week I’ma speak on vector fields On spheres — not clear how many fit when we ask them to be independent

The crystallographic restriction theorem says a finite-order automorphism of $\mathbb{Z}^3$ (in chemistry language, a symmetry of a crystal) has order $1$, $2$, $3$, $4$, or $6$. But $\mathbb{Z}^3$ is small potatoes; so let’s go to $\mathbb{Z}^n$, do some Galois theory in cyclotomic fields, and get us some icosahedral symmetry! (Icosahedrite is a real thing, say serious scientists.) Pretty pictures will be provided, including demonstrations of self-similarity. Self-similarity is always cool, right?

As any musician knows, you can hear the shape of a string — for a fixed material and tension, the fundamental frequency uniquely determines the length. As any musician also knows, drummers aren’t musicians (it’s ok — neither am I!). That’s probably because you can’t hear the shape of a drum. Are mathematicians musicians? Certainly not geometers — it turns out you can’t hear the shape of a hyperbolic surface either. What about number theorists? With trace formulas, eigenvalues, length spectra and more, find out the answer this week at PIZZA SEMINAR!

I will present the fact that for any polynomial $f$ of integer coefficients of degree grater than $1$, if $f$ is irreducible in $Q[x]$, than there are infinitely many prime numbers $p$ such that $f$ has no solution in $F_p$. Moreover, I will show that these prime numbers have positive natural density. As an example, I will compute the number of solutions of $x^3-x-1$ in $F_p$ for various $p$ and then relate these numbers to the coefficients of the $q$-expansion of a particular modular form.

I graduated from University of Chicago in 2008. My advisor was Drinfeld. I am currently a faculty member in Australia. I am visiting UChicago to talk about job hunting for mathematics students. I did my studies/postdocs in four different countries: Canada, USA, Germany, and Australia. I am familiar with the advantages and disadvantages of each. I had a lot of ups and downs in my career, but ended up with a job that I love. In addition, I am quite familiar with the attitudes of UChicago students regarding job market, etc. I am hoping that sharing my experience will help fellow UChicago graduate students plan their future better.

Postdocs Agnes Beaudry, Hung Vinh Tran, Ronen Mukamel, and Davide A. Reduzzi will share their wisdom about the job search process, adjusting to being a postdoc, and life after the postdoc. This is a great opportunity for both younger grad students and those nearing graduation to learn about the academic career path, and to get their questions answered.

We all know that the real function $e^{-x^2}$ does not have “an elementary antiderivative”. Other non elementary integrals are the famous elliptic integrals. But what does it mean to be non elementary? In this talk, we will define what it means to be integrated in elementary terms and give two criteria for a function not to have an elementary antiderivative. We will use these to prove that $\int e^{-x^2}\,dx$ is not an elemantary integral. All we will need is a little bit of field theory and complex analysis.

I will explain Grothendieck’s approach to proving the theorem for a proper morphism between two quasi-projective varieties over a field.

I will explain the phenomenon of orbit shadowing in hyperbolic dynamics with an example.

We’ll discuss how to describe systems which admit no description. At least not that I’d screw with. Not in this lifetime. Give up and frown upon Brownian motion. Derive Ito’s formula, aka the fundamental theorem of stochastic calculus, aka flex mcnasty, aka the 37th chamber, and affix a precise intuition to its mystical reality. Finally, describe the connection between differential equations and stochastic processes, better understand the processes and recall the beginning.

The interplay between functional analysis and geometry is a rich subject which has produced some of the crown jewels of 20th century mathematics. But I don’t like the word “bundle”, so we will do spectral graph theory instead. There will be pictures of graphs, analysis without deltas or epsilons and some hand-waving towards big fancy theorems at the end.

We explain via the canonical formalism of Hamilton why symplectic geometry is the natural mathematical framework for classical mechanics and prove a classical result of Noether relating symmetries and conserved quantities.

A cute application of ultrafilters.

Mathematician stuns audience with magic trick. What happens next will surprise you!

Ever wanted to learn what supersymmetry is really all about? Well, this isn’t really going to explain it, but it’s going to give you just enough that you can pretend to! We’ll start with a pseudo-explanation of quantum mechanics, turn to supersymmetry, and end up with the concept of adinkras.

All material beyond quantum mechanics comes from papers by Sylvester James Gates.

Error correcting codes are used when transmitting messages through noisy channels. For example, the ISBN is a code consisting of nine digits $a_i$ followed by a digit 0–9 or X corresponding to $\sum_i a_i \pmod{11}$. I will start by giving the definition of a code and proceed to give a few examples, including the binary Hamming code, which will be constructed using polynomials over a finite field. The Hamming code turns out to be an example of a Goppa code. These latter codes are constructed using linear systems on curves over finite fields. It turns out that curves with many rational points relative to their genus give rise to good codes. The Riemann Hypothesis gives a preliminary bound on the number of rational points for curves of fixed genus. Other bounds are discussed, and we will see how class field theory helps us come up with “good” codes.

Short version: see some cool arithmetic geometry applied to [a layman’s] real life. Get some ideas for what to write in your next NSF grant.

Have you seen a finite topological space? If so, do you know that they can have infinitely many non-trivial homotopy groups? Buckle up, because these spaces are gonna be legend … wait for it …

This is an introduction to Zariski’s main theorem.

We’ve all heard of the Four Color Theorem. Blah blah longstanding open problem blah blah computer-assisted proof blah. But did you know that it is equivalent to the fact that every snark is non-planar? (If so, you’d better bring some reading material.) This talk will cover some basic coloring problems in graph theory with a topological slant.

It’s one of those truly galling things to hear: Klein solved the quintic with an icosahedron in 1884. It makes it sound like Klein was playing D&D; in the basement of Gottingen when suddenly he glanced at the die and chuckled “My God, of course that’s how it’s done!”

We’ll start by talking about classifying $3$-manifolds by their fundamental groups, content ourselves with the finite fundamental group case, realize that we’ve stumbled into an ADE classification, then use some uber-classical algebraic geometry (Segre embedding, doubly ruled quadrics) to reduce solving the quintic to things we’ve serendipitously just discussed + the computation of some polynomial invariants. As per math talk etiquette, I will not compute in public.

The number $x^2 + x + 41$ is prime for all $x$! Hyperbolic manifolds have no rational points! A million proofs that there are no imaginary quadratic fields of class number $1$! Unravel these mysteries, and more, this week at *drumroll* *cartwheels* *lion taming* PIZZA SEMINAR!

The Schwarzian is a terrible looking formula but actually a beautiful piece of math. Come find out why I (geometer, general-calculus-hater-at-large) think it’s a delightful idea to spend a whole hour talking about something that involves third derivatives.

This talk starts with words like “what are the isometries of the circle?” and ends with words like “cocycle on the Virasoro lie algebra of smooth vector fields” and “complex structure on Teichmuller space”. In the middle, we’ll see some classical projective geometry (turns out that shit is really cool!) and a few other surprises.

Given positive integers $n$ and $k$, in how many ways can you write $n$ as the sum of $k$ squares? Looks like a simple enough question, but looks can be deceiving. We’ll discuss some cases of this question and we’ll see some of these pizza-seminar favourites come up: generating functions, class field theory, $L$-functions, quaternions, Fourier transforms, trace formulas, congruence subgroups, modular forms, Riemann–Roch, that picture of the upper-half plane tiled by semi-circle-triangles that everyone always draws, and more!

Despite their elementary foundations, generating functions are amazingly useful tools — with uses like solving recurrence relations, studying sequences’ asymptotics, computing statistics, and proving combinatorial identities. In this talk we’ll see some applications to binomial relations, symmetric group combinatorics, and random walks. There will be an overview of the basic theory for those who want a refresher, and some challenge problems for the more advanced.

Often times after a theorem about the complex numbers is proven in a book, a seemingly innocent claim follows: “the result holds equally well for arbitrary algebraically closed field of characteristic zero”. What if the proof uses structures of $\mathbb{C}$ other than being a field (e.g. uses topology or complex analysis)? In this talk, I will talk about the Lefschetz principle which justifies such a statement. This new perspective viewing algebraic objects, quite unexpectedly, comes from logic, or more precisely, model theory.

There is a long tradition when resolution of geometric questions requires us to depart the world of geometry and enlist the help of algebra. The oldest go back to the Greeks who were concerned with trisecting angles and constructing squares of equal area to a circle! Coming back to the present, we want to consider problems of the following nature:
“If a chessboard is covered by $21$ blocks of size $1 \times 3$, what are the possible locations for the remaining square?”
“Is it possible to tile a square with an odd number of triangles, all of which have the same area?”

As it turns out, the first one ends up being settled with the aid of the group ring and cyclotomic fields, and the second one leads us to call on valuation theory and Sperner’s lemma. In the upcoming talk, we will discuss some of the algebraic methods used to solve such tiling and related problems.

In this talk, I will explain the connections between Lefschetz fibrations, symplectic $4$-manifolds and mapping class groups. In particular, I will talk about monodromies of symplectic Lefschetz fibrations and factorizations in mapping class groups, and survey some classification results on low-genus Lefschetz fibrations. If time permits, I will present an example due to D. Auroux which suggests a new approach to distinguish homeomorphic surfaces of general type.

Have you ever wondered how Google Translate works? Well, that’s still a secret. But earlier this year researchers at the Googleplex published several papers on the arxiv in which they mapped words to a high-dimensional vector space and used linear transformations to translate between English-space and, say, Czech-space. Maybe linear algebra won’t supplant the sophisticated statistical models anytime soon, but the authors are shopping it at least as a quick way of scanning dictionaries for questionable entries. Come find out what happens when you project the numbers 1 through 5 onto a plane, and a bit about how neural networks work.

You and several other players are offered a chance at a game. Each of you will have either a red hat or a black hat placed on your head, uniformly and independently at random, then you will be allowed to see each other but not communicate, finally and simultaneously each person must either guess the color of their hat or pass. If there is at least one correct guess and no incorrect guesses, you each win a million dollars. What’s an optimal strategy, how often does it win, and what does this have to do with Hamming codes? For the purposes of this talk, hats will be replaced with playing cards and \$1,000,000 will be represented by a piece of candy.

A group action on a space (manifold) usually gives us some insight into properties of the space (manifold). The situations get even better if the group, the action, or the manifold is decorated with adjectives such as compact, Lie, algebraic, smooth, symplectic, Hamiltonian, etc. Morse theory is also another powerful tool to extract information about the topology of smooth manifolds. In this talk I will introduce the notion of a moment map for a group action on a symplectic manifold and give a brief survey of what it can be used for. I will also give a quick introduction to Morse(–Bott) theory and talk about connections with the moment map.

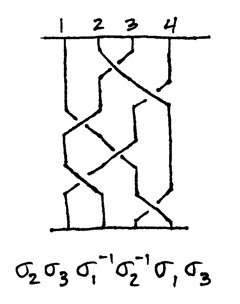
If we just told you straight up that this week’s pizza seminar talk was going to be about math and magic tricks, you’d probably think it would be about as cool and/or interesting as this guy: But what if we told you that we’d be talking about a magic trick invented by this guy: And that this was some of the math involved: 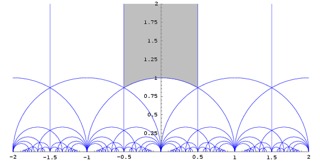Then you’d probably want to come.

We will be talking about low-dimensional affine and projective geometry. In particular, we will interest ourselves in the axiomatic characterizations of projective and affine geometries, how Desargues’s theorem on perspectivity of triangles relates to the classification of projective geometries in higher dimensions, and what goes wrong in dimension $2$.

Let $f$ be a polynomial with integer coefficients. How many solutions does $f = 0$ have modulo each prime? The answer is given by reciprocity laws (some established and some conjectural). I’ll begin with several examples before discussing the connection between this question and Galois representations, $L$-functions, and automorphic forms.

The axiom of choice is nice and all, but it lets us do some pretty terrible things (Banach–Tarski, anyone?). Wouldn’t it be nice to have some way to prevent these pathologies from happening? A few weeks ago, Jonny mentioned the axiom of determinacy, which does exactly that … with games! I’ll be talking about what exactly the axiom is, how it gets rid of a lot of the pathologies that choice gives us, and how we can use it to get a handle on just how simple these pathological sets could possibly get.

How do properties of convex subsets of $\mathbb{R}^n$ interact with number theory? How about trying to find integer points in convex sets; for example, $0$ is the only integer point contained in the open cube $(-1,1)^n$ (this is not so hard to prove, actually). Now, what property on the volume of such a set could ensure that this set contains at least one integer point? The answer, given by Minkowski’s theorem (and this is harder), proven in 1889, initiated what is today called the “Geometry of Numbers”. We will give two proofs of this theorem, one geometric and one analytic, and discuss how this can be applied to a couple of number theory problems: Dirichlet’s approximation theorem and Lagrange’s four square theorem.

Imagine oranges stacked at a grocery store. Is this the most space-efficient stacking pattern? This is the famous Kepler conjecture, originally formulated in 1611, and in 1900 reformulated as part of Hilbert’s eighteenth problem. Intuition says yes, but the proof remained elusive for some centuries, until Thomas Hales gave a computer-assisted proof in 1998. Since this question is much too difficult for us to address, we turn to a related but much simpler problem. Each orange in the interior of the stack touches $12$ other oranges. Is it possible to arrange $13$ oranges around a central one in such a way that they just touch the central orange? This is the famous problem of thirteen spheres, and was a subject of a discussion between Isaac Newton and David Gregory in 1694. Newton believed $13$ oranges was impossible. Gregory thought otherwise. Following a proof by John Leech, we answer the question in the negative: $12$ is the maximal number. We will then briefly discuss a higher-dimensional generalization, the so-called kissing number problem.

By and large, mathematicians like to work with sets. We’re comfortable with them. We might even think of them as objects that have some real existence.

To make the idea of a set precise, we have a system of axioms called ZFC, which models the behaviour we expect of sets. However, this leads to some problems: the system (if it’s consistent) has many different models. Questions like “does the continuum hypothesis hold?” have answers that depend on which model we consider.

For a long time, this sort of phenomenon was seen as the price we have to pay for our formalism. However, we’d prefer to choose one specific model that’s acceptable to everyone, so that we don’t have to worry about that sort of thing — and (as of this decade) it seems like it might be possible.

Set theory began in 1873, and is still happening. Let’s pay a visit.

Have you ever seen a square wheeled bicycle? If not, here’s a very serious picture. When I saw this, I wondered if you could make a regular-$n$-gon wheeled bicycle that would roll just as smoothly, given the right road. What about an arbitrary polygon? What if I give you a crazy periodic curve for a road — can you build me a wheel to roll along it? Will the wheel be unique? Will you still travel at constant speed if you pedal at a constant rate? Luckily, we know math, so we can find the answers to these pressing questions.

Prerequisite: watching some youtube videos of people riding square wheeled bikes and tricycles.

Tropical algebraic curves are relatives of classical (complex, say) curves constructed over the so-called tropical semi-ring. They are combinatorial objects, hence much easier to understand than the classical ones, but most of the classical results survive in the tropicalized theory, often acquiring some cute combinatorial interpretation. In this talk I will state and explain the tropical versions of some classical theorems, and hopefully no background in algebraic curves is required.

We will start by bouncing a ball in a polygon, proceed through some physics and dynamics, and end up with rigid curves in moduli space giving new and special polygons. There will be the opportunity to win fame and fortune by answer a question about triangles that you could have understood in grade school.

Apparently some people have real jobs and this involves having to do things efficiently. We’ll look at one example of how this is sometimes hard; the travelling salesman problem. Interestingly, the problem becomes easier (that is to say there is a known solution) when we pass from the discrete to the continuous. This is the “Analyst’s Travelling Salesman” problem and in solving it we will see some conformal geometry, geometric measure theory and harmonic analysis (of course no knowledge of any of these things will be assumed).

In this talk, I will start with the definition and basic properties of the homotopy groups of spheres, and then talk about their connections with Poincaré conjectures, cobordisms and derived algebraic geometry (if time allows).

I will explain A. Schoenhage’s algorithm that allows to multiply two $3$ by $3$ matrices using only $21$ multiplication operations, resulting in a matrix with entries within any given number $c$ from the entries of the actual answer. In order to explain this algorithm, I will show how to reinterpret it as a search for limit points on secant varieties of a Segre embedding.

You know what’s great about knowing math? You can prove (yes, pretty much prove) that sexual reproduction kicks butt — on a grand evolutionary scale — compared to the far less fun asexual alternative.

Starting from some really elementary assumptions, we’ll get a model for information acquisition through evolution (whatever that means), plug in some elementary probability theory, and conclude that sex generally wins over no sex, especially in unstable environments. Applied math FTW.

Disclaimers:
1. Any probability theory involved will be easy enough for a geometer to understand.
2. You might learn something about the physical world, or at least how science understands it.
3. This talk is largely modeled after a book chapter by the same name in Mackay’s “information theory, inference and learning algorithms”. Highly recommended.

Let $S$ be a closed surface, and let $f$ be any homeomorphism of $S$ to itself. Is there a classification of the types of behavior that $S$ can exhibit? Of course not — the homeomorphism group is absurdly large, and there are homeos doing arbitrarily crazy things in arbitrarily small neighborhoods. But what if you allow yourself to adjust your homeomorphism by an isotopy? The remarkable answer here, known to Nielsen and first proved by Thurston, is that there exists a complete classification of homeomorphisms up to isotopy, and that any $f$ is isotopic to one of only three specific possibilities. I’ll explain this result, which will take us on a brief tour of the mapping class group and of Teichmüller space, and discuss some applications to geometry and topology.

I will give an introduction to toric varieties and describe how to build them by drawing pictures. The structure of these varieties has been extensively studied. In fact we can extract a lot of information about a toric variety just by staring at its corresponding picture. This makes toric varieties particularly convenient to compute with.

The talk will feature some algebra, various^* kinds of geometry, and lots of pictures.

*at least two

Special values of zeta functions are conjectured to have deep arithmetic meaning. Euler discovered that special values of the Riemann zeta function satisfy mysterious congruences. I’ll explain these congruences using measure theory! (I might be overselling the analysis involved.)

This very second $10^14$ (plus or minus a few dozen trillion) photons are entering your eyes, letting you read this abstract. In this pizza seminar I will talk about the mathematics behind these particles, Schrödinger equation. Along the way we’ll look at the history and development of this theory as well as the interpretations of what the theory predicts.

Welfare economics is a branch of economics associated with aggregating individual preferences into a social preference. Sometimes that’s impossible to do nicely, as in Arrow’s Theorem (see Yiwei’s talk last year), but sometimes we can get exactly what we want — and for that, we need geometric Hahn–Banach.

The interval between two pitches sounds nice when the ratio of their frequencies is a ratio of small integers. An octave is a ratio of $2:1$, so to get the $12$-note chromatic scale we just split that evenly — a half-step is a ratio of $2^{1/12}:1$. Seven half-steps make a perfect fifth, which is a ratio of $2^{7/12}:1 = 3:2$… we wish. Sadly, you can even hear the difference! But I heard that continued fractions lead to good approximations by rationals, so maybe we can do better with a different number than $12$.

In this talk, we’ll think about the equation $x^n+2y^n=1$ (and others like it) and ask “how many integer solutions $x$ and $y$ does it have?” We’ll explore two different methods for attacking this type of problem: the first uses the fact that algebraic numbers aren’t very well approximated by rationals (what?!), and the second uses geometry, somehow.

The chip firing game offer a fascinating bridge between combinatorial and algebraic objects. In this talk, I will introduce the chip firing game on a directed multigraph and discuss connections with lattice ideals. In the undirected case, there is a fabulous interplay between combinatorial data in the graph and algebraic information in the corresponding “toppling ideal.” In particular, we can use the graph structure to give an explicit minimal free resolution.

Simplicial objects play an important role in fields such as algebraic topology, algebraic geometry. Even Drinfel’d was amazed by how fundamental this thing is for some of his work. I will do some basic definitions and use them to construct classifying spaces of groups we know and love. This is not rocket science!

John Baez describes the octonions as “that crazy old uncle nobody lets out of the attic”. In this talk we’ll define this eccentric non-associative algebra and describe its connection to Bott periodicity and exceptional Lie groups.

To celebrate Halloween, I will tell a story about the Monster group. This starts with the important observation (by John McKay) that $196884 = 196883 + 1$.

Here, of course, $196883$ is the smallest dimension of a faithful representation of the Monster group, and $196884$ is the first nontrivial coefficient of a certain modular function associated to $\mathrm{SL}(2,\mathbb{Z})$. This was generalized by Conway and Norton to other fun identities such as $864299970 = 842609326 + 21296876 + 2 \times 196883 + 2 \times 1$.

Based on this, Conway and Norton formulated the ‘Monstrous Moonshine conjecture’ (later proven by Borcherds), which explains the relation between the Monster group and modular forms on $\mathrm{SL}(2,\mathbb{Z})$. I will show where this connection comes from, and we’ll discover that the Monster group is quite the beautiful creature after all!

Schur functors could be defined for a general Karoubian tensor category, but the most interesting and classical application is still that of constructing new group representations from old ones. In this setup there exists an almost purely combinatorial correspondence between $S_n$-rep and (part of) $\mathrm{GL}_k$-rep known as the Schur–Weyl duality. In this talk I will talk about a natural generalization of this phenomenon first studied by Roger Howe. There will be some exciting applications.

N/A

The ancient greeks struggled for centuries with straightedge and compas constructions. Amongst their greatest challenges was trisecting an arbitrary angle (a task which was much later proved impossible with straightedge and compass). In this talk we strike a blow against the western hegemony and use origami to simply trisect arbitrary angles. Along the way we’ll talk about some Galois theory and do some folding. Origami paper will be provided.

We will determine the price you pay to bet on the stock market. Specifically, we will determine the price of so-called European options. Simply, after say a week, the value of a stock will either go up or go down, and you can bet on it. The price you pay for the opportunity is determined by the Black–Scholes equation, which we will derive following an informal discussion of Brownian motion, stochastic calculus and stock market gambling.

A combinatorial game is a two-player game of no chance and perfect information. In analyzing these games we stumble upon many beautiful objects, for example the surreal numbers, which is a field (that is, it would be if it were a set) including both the real numbers and the ordinals. But combinatorial games have many more surprises in store for you. As do I.

A classic theorem of number theory due to Szemerédi states that every set of natural numbers of “positive density” contains arbitrarily long arithmetic progressions. The case of three-term arithmetic progressions follows quickly from the innocent-seeming triangle removal lemma, an approach which was recently generalized to $k$-term arithmetic progressions. In this talk, I will discuss aspects of a proof of Szemerédi’s theorem, and connections to graph theory. Szemerédi’s regularity lemma, which puts a “pseudorandom” structure on arbitrary graphs, will be central to everything.

Does the equation $y^3=5+x^2$ have integer solutions? The answer is no, but if you try to do it by hand, most probably you won’t be succesful. The reason is that the ring of integers of $\mathbb{Q}(\sqrt{-5})$ is not a PID.

In this talk I will discuss the classical problem of number theory, about how far the ring of integers of algebraic number fields are from being Unique Factorization Domains. Namely, I will define the ideal class group of a Dedekind domain and then we will see that in the case of the ring of integers of an algebraic number field this group is always finite. The fact that the order is $2$ in the case of the quadratic field $\mathbb{Q}(\sqrt{-5})$, will play the crucial role in the nonsolvability of the previous equation.

Postdocs Tuca Auffinger, Jon Chaika, Angélica Osorno, and Artem Pulemotov will share their wisdom about the job search process, adjusting to being a postdoc, life after the postdoc, and whatever else the audience wants to know.

This is a great opportunity for both younger grad students and those nearing graduation to learn about the academic career path, and to get their questions answered. We hope to see everyone there!

Renormalization is a technique that’s widely used in dynamical systems, statistical physics, probability, PDEs or anything else that involves some analysis. I will start by giving a heuristic for how the method works and then I will work out several examples from very different areas. Diophantine approximation, lattice models, the logistic family and the Central Limit Theorem are some examples that I hope to cover.

Did you know that most things you work with are too big? Simply too big, far too much, and a great deal too many. By introducing some axioms for clearing up this infinite clutter we spend much of our time embroiled in, internal set theory provides a framework in which many of the concepts and proofs that we use all the time are cleaning and more intuitive; examples will hopefully be persuasive. Sadly there are some costs, mostly in the form of ridiculous sounding consequences; examples will hopefully be controversial and borderline offensive. I will conclude with vague gesturing at a proof that this is not a bunch of hooey.

Warning: this talk may contain some set theory.

Given a finitely generated group $G$, one can build the Cayley graph of $G$ and use the word metric to make it into a metric space. Geometric group theory studies how the algebraic properties of $G$ influence and are influenced by the geometry of the Cayley graph. I will prove a classical theorem by Milnor and Wolf, classifying the (virtually) nilpotent groups among all solvable groups by their geometry.

(Now seems a good time to shamelessly advertise my FFSS talk on Thursday [4:15 pm in E308] in which I will talk about Gromov’s amazing generalization, recognizing the virtually nilpotent groups among all finitely generated groups by their geometry.)

Algebraic objects are often given “biased” definitions — defined in terms of one or two operations satisfying relations. I will discuss monads and operads, two tools which allow discuss algebraic objects in an “unbiased” way, in which every possible operation is treated identically by the formalism. Examples and applications will hopefully be plentiful.

What is the number of proper $k$-colourings of a given graph, as a function of $k$? A perhaps non-obvious fact is that this is a polynomial, called the chromatic polynomial of the graph. I will explain a beautiful proof of this fact using Möbius inversion (which we will learn along the way).

As a bonus, I may talk about one or two other examples of slick proofs that use Möbius inversion.

Let $X$ be a closed surface of constant curvature. Then the Weyl’s law states that $N(t)\sim (t\cdot Area(X))/4\pi$, where $N(t)$ is the counting function of Laplacian eigenvalues on $X$. In this talk I’ll sketch an algebraic proof based on a simple version of the trace formula.

In a year of elections worldwide, we may ask ourselves, does it really matter who we vote for? We use current events in Russia as an illuminating example.

The Robinson–Schensted–Knuth correspondence is a classical combinatorial result that everyone should know. It has a nice symmetry property which is not at all obvious at first glance from the usual algorithm. Surprisingly, there’s another algorithm, due to Fomin, which uses so called ‘growth diagrams’, which gives the same correspondence and for which symmetry becomes obvious.

More precisely, what I am actually going to do is that I will draw some boxes, put numbers in them and then move them around and magic will happen!

In some sense, buildings are a higher-dimensional generalization of trees. We’ll use the example of trees to get a clear, mostly combinatorial presentation of the definition. Then we’ll talk about spaces that happen to be buildings, notably the Tits boundary of a symmetric space.

Mark Kac famously posed the question above in a 1966 article, although similar questions had been asked before. John Milnor showed almost right away that the answer is no, not if you listen to $16$-dimensional torus drums, but for the rest of us, the question wasn’t resolved until 1992. I’ll explain what on earth the question means, and how it got answered in the end.

Gödel’s incompleteness theorems say that any nice enough and strong enough logical system is incomplete (that is, has statements that are not provably true or false), and that no such system can prove its own consistency. We’ll be showing how to prove these by taking common paradoxes and formalizing them using Kolmogorov complexity: Berry’s paradox (“the smallest natural number than can’t be described in fewer than thirty words”) gives us a way to prove the first incompleteness theorem, while the surprise examination paradox (“the pop quiz can’t be on Friday, because then it wouldn’t be a surprise…”) lets us prove the second incompleteness theorem. We’ll then turn things around and see what the incompleteness of arithmetic has to say about resolving the paradoxes.

What’s your favorite experience of the integers? Perhaps you enjoy its additive structure or that it contains solutions to $x^2+y^2=z^2$. Ramsey theory asks, “Are such properties preserved under finite partition?” We discuss some Ramsey theoretical results and an approach through ergodic theory.

an introduction to algebraic geometry

Given four skew lines in $3$-space, how many lines intersect all four? The answer is two^*! Problems of this nature are called enumerative problems in algebraic geometry and often require sophisticated calculations. This one is simple enough that I will give two proofs of this fact: one using elementary algebraic geometry and one using intersection theory on a Grassmannian. No rings or schemes required!

*sort of.

Don’t you love thinking about lines? I do. The FTPG is all about lines. We will prove the baby case, which says that a bijection of R^n taking lines to lines must be linear. (Go figure.) Then we’ll take a gander at the general statement of the FTPG, with perhaps some indication its proof on the side. Time permitting, we will define “buildings” and state Tits’ big generalization of the FTPG.

We have all done measure theory courses and know how to integrate with respect to a measure. In this pizza seminar we instead will consider integrating with respect to the Euler characteristic. We will see that there is a well defined calculus theory if we restrict to “constructible functions” - we even get Fubini’s theorem. This Euler calculus will then be applied to the problem of target enumeration for both stationary and moving targets (this means counting how many targets from a function that tells us at each point how many targets we can see.)

This talk is meant to be an introduction to the notion of entropy in dynamical systems. We will define topological and metric entropy and discuss their relationship to other dynamical concepts (in particular, Lyapunov exponents). Geometric and probabilistic examples will be provided. This talk will be a short tasting of dynamical systems, ergodic theory, geometry, probability, and pizza of course.

In past pizza seminars we have seen the hyperbolic plane. Because it turns out the hyperbolic plane is pretty nice to work with, we define a group to be hyperbolic if it looks like the hyperbolic plane (in some sense). I’ll give some examples, and show a few of the remarkable implications for the group structure.

Hopefully, all of you care about invariants of topological spaces. I intend to motivate and introduce the stable homotopy category, which can be more informally be called “the place where cohomology theories live”. I will say some words about ordinary cohomology, which you may or may not remember from the first year, and then I will gloss over decades of work by forgetting one of the Eilenberg–Steenrod axioms. This will give a conceptual outline of the general picture, after which I will attempt to convince you as to why such a perspective is useful.

Dilogarithm is like a logarithm, except somewhere in a definition of logarithm, you change a $1$ to a $2$. You might think, “that’s a completely arbitrary thing to do, why would you do that?” Well, the answer is that lots of smart people have done it before. Dilogarthims have been used by Milnor and Thurston to study hyperbolic geometry, by Bloch to study $K$-theory, by Coleman to study explicit reciprocity laws and $L$-functions, by Kirillov to study physics, and by Deligne and Beilinson to study motives.

In this talk, I’ll explain how to get from $K$-theory to hyperbolic $3$-manifolds and Mostow rigidity to zeta functions of quadratic imaginary fields — all through dilogarithm.

Basic physical concepts will be recalled and applied to the motion of a spinning top. The motion is readily observed to consist of three periodic cycles. The cycles are shown to be intrinsic to the motion, not the result of external torque. That is, a top spins in space as it does here.

Time permitting Noether’s theorem and Poincare recurrence will be discussed in this setting.

Sometimes there is a bunch of candy somewhere (like in other peoples houses), and sometimes you want this candy to be elsewhere (like in your house), but moving candy isn’t easy. Finding the best way to get your candy from their house to yours is a question of optimal transport. Thinking about what this optimal transport is can be hard, but thankfully just its existence (which we will assert without proof) can be very useful. As an example, we will prove the isoperimetric inequality using nothing but some mathematical facts you might find lying around your kitchen, with sufficient generality to extend trivially to the anisotropic isoperimetric inequality, which is fun to say.

The talk will center around the problem of when you can extend a bounded holomorphic function to a removed compact set. If that sounds boring to you don’t worry; the talk is really about geometric measure theory and how it is super cool! There will be Hausdorff measure, rectifiable sets and maybe (if everyone behaves) tangent measures!! If that still sounds boring to you still don’t worry; at least there will be pizza.

The Crofton formula says the length of a plane curve is equal to the “expected” number of its intersections with a random straight line. In the talk I’ll include some applications and generalizations.

Combinatorial games are a special type of two-player game defined by J.H. Conway. Wikipedia has this to say on the matter: “Combinatorial game theory (CGT) is a branch of applied mathematics and theoretical computer science that studies sequential games with perfect information, that is, two-player games which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning condition.”

Now, the obvious question is: what does this have to do with category theory? If you want to find out, come to Pizza seminar tomorrow!

By the end of my talk, you should be able to understand — better yet, appreciate — a recent result of our own Howie Masur and Jon Chaika, along with Yitwah Cheung. The talk is about Schmidt games, what it means to win them, how you can beat me at them (yes you can), and how they relates to badly approximable real numbers, hyperbolic space (!), and (!!) Teichmuller geodesics. Despite the words “Teichmuller geodesics” above, this talk should be non-scary.

P.S. The paper in question is: http://arxiv.org/abs/1109.5976.

P.P.S. I don’t recommend you try to read it before pizza seminar.

I will try to explain how one can find the roots of a general polynomial of degree five. We shall use tools from dynamical systems, algebraic geometry, representation theory and analysis. The talk will be very accessible (I promise).

Postdocs William Lopes, Angélica Osorno, and Vlad Vicol will share their wisdom about the job search process, adjusting to being a postdoc, life after the postdoc, and whatever else the audience wants to know.

This is a great opportunity for both younger grad students and those nearing graduation to learn about the academic career path, and to get their questions answered. We hope to see everyone there!

An expander graph is a highly connected sparse finite graph; examples which come to mind are nerve cells in the brain, a robust computer network, and social networks. The existence of expander graphs follows easily from a probabilistic standpoint, but explicit constructions have required Kazhdan’s Property $T$ or the Ramanujan–Petersson conjecture. In my talk, I will introduce expander graphs and Ramanujan graphs. Then I will proceed to talk about the construction of expander graphs from Kazhdan’s Property $T$. You can expect to see plenty of graphs.

Anna Marie Bohmann discusses stirring things up on surfaces, a la Spencer Dowdall. Pretty pictures are included.

Emily Riehl discusses how to do equivariant algebraic topology for all groups at once, a la Anna Marie Bohmann.

Tom Church discusses model structures with extra structure — no prerequisites necessary — a la Emily Riehl.

We know a fair amount about groups of homeomorphisms of the line. The plane is a different story. In my talk, I’ll give some examples of seemingly elementary questions that we have no idea how to solve, as well as some that have been solved only very recently. If you’re lucky, I’ll also give a proof of one thing we do know about homeomorphisms of the plane, the Brouwer plane translation theorem. It was proved in 1912 and it’s still a cutting edge tool in the study of group actions on the plane.

Though the Littlewood Richardson Coefficients were introduced in 1934 as a means of computing characters of representations of the symmetric group, these coefficients have since appeared in the answers to questions in surprisingly diverse areas of mathematics. We will look at some of the places they have arisen, as well as a method of calculating these coefficients. Time permitting, we will survey their relevance to the recently completed work of Knutsen, Tao, and Woodward on determining the possible eigenvalues of a sum of Hermitian matrices.

This talk will have very few proofs, but lots of little boxes.

It is the dream of every young mathematician, gazing wearily out the window in ninth grade, to someday have their own constant, like Euler, Archimedes, Conway, or Euler–Mascheroni (the more pasta like of Euler’s two constants). Well I still don’t have a constant and neither do you, but Khinchin does! It’s about 2.685. Why is that number better than any number you were the first one to think of? You can either google it or come to pizza seminar. Since only one of those comes with pizza, I think the best course of action is clear.

The motion of a surface by its mean curvature will eventually be discussed. Indeed, the evolution may be defined for an arbitrary compact set. Foremost, however, is to determine why anybody talks about it. It will be shown that the pressure differential across a membrane determines its mean curvature and, in particular, that soap films form minimal surfaces. Applications of mean curvature flow to image processing will be mentioned.

Last quarter, Anna Marie tried to convince you what an extraordinary construction topological $K$-theory is. Now I will try to convince you how extraordinary algebraic $K$-theory is also. There will be lots of algebra, topology, number theory, category theory, and at some point even a limit (not a categorical one) will appear to make the analysts happy.

Every spring Peter May tries to teach all of category theory in three lectures. This year I plan to do him one better and teach all of category theory in a single lecture^*. To be fair, my task is rather simplified by the famous observation of MacLane that “all concepts are Kan extensions.”

In part I, I’ll give the simple definition of left and right Kan extensions and then state an incredibly useful formula^** which defines Kan extensions pointwise. After the break, I’ll cover all concepts — or at least limits/colimits, adjunctions, and the Yoneda lemma.

*And I won’t even go over time.

**Completely seriously this is the only reason I know how to define geometric realization, or extension of scalars, or induced representations, or derived functors.

Suppose you are at a soccer match and some group in the audience begins to start the wave. As another member of the audience, your decision to stay seated and stand up is based on trying to optimize your position in the wave, as well as considering the positions of those around you. This is a canonical model for a mean field game, which is a system of partial differential equations meant to describe an optimization problem depending on the behavior of multiple (and eventually infinitely many) agents. This talk will be an introduction to mean field games, which some of you may note is a common topic Pierre-Louis Lions comes to talk about. In this talk, I will describe Hamilton–Jacobi equations, Fokker–Planck equations, and the coupling that happens between them in a mean field game.

We’ll discuss the title question as well as related questions such as “what does that even mean?” and “who cares?” In the process we’ll define computation over a general ring, with the usual theory of computation as a special case. No previous knowledge of computability necessary.

The Hopf invariant of a map from $S^{2n-1}$ to $S^n$ can be used to study related questions in algebra (When can $\mathbb{R}^n$ be a division algebra?) and topology (When does $S^{n-1}$ have a trivial tangent bundle?). I will give an overview of this relationship, and sketch a proof due to Adams and Atiyah of the fact that $n=1$, $2$, $4$, $8$ are the only possible values. This will use only the basic structure of complex $K$-theory. This realization helped motivate the development of modern stable homotopy theory.

Topological $K$-theory was the first “extraordinary” cohomology theory to be discovered, and it remains a fundamental tool in algebraic topology today. I will introduce topological $K$-theory, starting from concrete considerations, and discuss Bott periodicity. For those of you who recall Niles Johnson’s applications of $K$-theory to astronomy in a pizza seminar of several years back, please note that my talk will contain a similiar application to $K$-theory to lexicography.

The infamous modular curve is the quotient of the upper half plane by the modular group $SL(2,\mathbb{Z})$. We’ll consider geodesics on this space and try to understand their dynamical behavior. It turns out this has deep (read ‘elementary but cool’) connections to continued fraction expansions. Using this connection we’ll answer questions like: Are there geodesics that stay in a compact set? What about closed geodesics, or geodesics that return to a compact part infinitely often? Can you find a dense geodesic? All this and more at pizza seminar this week!

When you learn abstract algebra, they talk about division algebras, but in real life, no one’s ever heard of any (except quaternions). I’ll talk about why there aren’t many division algebras; there’ll be some Brauer Groups, a few polynomials, and a splash of Galois cohomology.

Semigroup theory is a classical, abstract tool used to solve differential equations. This talk is meant to be an introduction to the subject. Topics will include basic definitions, properties, and the Hille–Yosida theorem. If time permits, I will discuss applications of semigroup methods to nonlinear PDE.

I’ll talk about the Brunn–Minkowski Inequality (which looks like the usual Minkowski inequality, but for volumes of sets) and its relation to the isoperimetric inequality. If time permits, I’ll also talk about the “length of a potato”.

I think the title pretty much says it all.

I will first give a very brief introduction to model theory. In particular, I will try to make it clear that model theory is mathematics, not meta-mathematics (although it certainly has applications to the latter, which I may not address at all). Then, I will show how the model theory of fields can be applied to prove statements like the following: Any injective polynomial map from $\mathbb{C}^n$ to $\mathbb{C}^n$ is surjective. If $k$ is an algebraically closed field, $K$ an algebraically closed extension, and $A$ a $k$-algebra, then [statement] holds for $A$ iff it holds for $A \otimes K$. (“Statement” can be “$A$ is an integral domain”, “$A$ is integrally closed”, …)

Disclaimer: I am not a model theorist, nor any other sort of logician, and have never taken a course or read a book on model theory.

Last year, I gave a pizza seminar talk on why people who care about statistical mechanics should care about braided monoidal categories. To my horror, I discovered that not everybody here cares about statistical mechanics! So as a second attempt, I’m going to explain why people who care about $3$-manifolds should care about braided monoidal categories. (Don’t tell me you don’t care about $3$-manifolds!)

Lickorish showed that every closed, oriented $3$-manifold can be obtained from a framed link in the $3$-sphere by a process called Dehn surgery. Two such manifolds will be equivalent if and only if the links are related by the so-called Kirby moves. So any invariant of framed links that doesn’t change under Kirby moves gives rise to an invariant of closed, oriented $3$-manifolds. Invariants of framed links live, in a very natural sense, in ribbon categories, which are braided monoidal categories with a bit of extra structure. I will explain what all of these terms mean, and I will sketch the construction, due to Reshetikhin and Turaev, of a $3$-manifold invariant that comes from any particularly nice ribbon category.

At one time or another, you’ve probably done some sort of construction with a compass and straightedge like dropping a perpendicular or bisecting an angle. We’ll describe all the things you can construct with these tools, and see what you can construct when you’re missing some of them. And then we’ll see exactly what you can do with your credit card.

The underlying problem of the Weil Conjectures goes back to some of the oldest questions in number theory. The problem is this: count the number of solutions to a polynomial modulo $p$. For example: $x^2-a=0 \mod p$, or $ax^2-by^2 = 1 \mod p$. How many solutions are there? What happens as I change $p$? What if I ask for several equations to hold simultaneously?

The Weil Conjectures (proven by Dwork (1960), Grothendieck (1965), and Deligne (1974)) are the result of thinking of these questions in the world of algebraic geometry and algebraic topology. We state the Weil Conjectures and discuss some of the ideas used to prove them.

Multiplying two matrices is dirt easy, and we all learned how do to it in time immemorial. But it turns out we learned a stupid^** way! There are much better ways to multiply matrices. I will discuss some of these better ways, as well as the significant role algebraic geometry and representation theory play in the computational complexity of matrix multiplication. Time permitting, I will discuss how the very same algebro-geometric and representation-theoretic ideas form the core of the only current approach to resolving much bigger questions in complexity, like permanent versus determinant and P vs NP.

* And by “heaven” I may mean “Volker Strassen’s office in Germany in the 1970s.”

** Slow.

One can profit greatly by making a Morse-theoretic analysis of the topology of algebraic manifolds. However it is possible to introduce an algebraic version of a Morse function to understand some of the most interesting elementary aspects of their topology without leaving the universe of algebraic geometry. Starting essentially from scratch, I’ll introduce Lefschetz pencils, and use their level sets to reveal the famous vanishing cycles. If there is time I’ll argue the Lefschetz hyperplane theorem geometrically.

Ladies and Gentlefolk, you are cordially invited to witness a slight of hand of the most sensational sort: the division of one ball into two of equal size using nothing but Euclidean motions and the axiom of choice. Amaze at the non-constructable sets. Learn to perform this trick yourself, guaranteed to confound at parties.^*

*Not guaranteed.

You hopefully can remember Ben’s talk on Morse theory three weeks ago. Discrete Morse theory is a version of Morse theory for maps from simplicial complexes (constant on each cell). There are many analogous result in discrete Morse theory to its smooth cousin. This talk will discuss a few of them.

Let $G$ be a $d$-regular (every vertex has $d$ edges) graph with no cycles of length $4$ or less, with the minimum possible amount of vertices $1+d^2$. Then $d$ is one of the folllowing numbers: $1$, $2$, $3$, $7$ or $57$! If you have a soft spot for Grothendieck’s prime, this is the talk for you! Also, if you need ideas for your research, an open problem will be stated.

Disclaimer: This is shamelessly stolen from Lazlo Babai’s REU class.

When solving an ordinary differential equation (ODE) the basic strategy of constructing solutions uses contraction mapping principle on a suitable complete metric space. This method works as long as we look for local solutions (defined on an interval $[0,T]$) and we are ready to allow $T$ to be small. As a payback for this restriction, we are able to establish a number of good properties for the equation. Not only do we get the existence of a solution, but a solution so obtained is unique in the complete metric space above and depends smoothly on the given data. Collectively, existence, uniqueness and smooth dependence is referred to as (smooth) well-posedness.

This basic strategy works surprisingly well for many partial differential equations, particularly “semi-linear” ones, where non-linear terms are of “lower order”. However, when one tries to establish well-posedness for more more non-linear “quasi-linear” initial value problems, where the “top order” terms depend on the solution, it is still often possible to establish existence, uniqueness and even continuous dependence on the data, but one is ofter forced to give up the smooth dependence on data. As a consequence the contraction mapping principle is not directly suitable to study such problems.

In this talk, I want to illustrate the difficulties with the quasilinear equations and methods of their analysis with a simple example.

The tools of Morse theory provide an extraordinary insight into the global topology of smooth manifolds. After developing the theory, we will observe almost as afterthoughts that every smooth manifold has the homotopy type of a CW-complex. And, that the summed indices of a vector field with isolated zeros is necessarily the manifold’s Euler-characteristic. This talk will emphasize the foundations of finite-dimensional Morse theory.

That is, given a manifold and a generic smooth function we will determine the manifold’s topology through a simple analysis of the function’s critical points. The development is concrete. To emphasize this we will show that a compact manifold admitting a generic smooth function with exactly two critical points is necessarily homeomorphic to the sphere. Time-permitting, applications of these ideas to certain infinite-dimensional spaces or to the development of homology theories will be mentioned if only briefly.

Define a sequence of integers by $a_0 = 3$, $a_1 = 0$, $a_2 = 2$, and then recursively by $a_{n+3} = a_n + a_{n+1}$. Calculate out a few terms, or a few thousand, and you’ll notice a curious pattern: the $n$th term $a_n$ is divisible by $n$ exactly when $n$ is prime!

The first counter-example is $n = 271441$, for which $a_n$ has over thirty thousand digits. I’ll explain why this coincidence holds so often, why it had to fail sometime, and why it takes so long to find a counterexample. The proofs will mostly just involve graphs, paths, polynomials, and matrices.