Geometry of Uniform Meandric Systems
from LQG and SLE viewpoints
Minjae Park
(University of Chicago)
Based on the joint work with Jacopo Borga and Ewain Gwynne
Glossary
- Meandric systems: Borga's talk
- SLE\(_{\kappa=8}\): scaling limit of uniform spanning tree peano curve
- LQG\(_{\gamma=\sqrt{2}}\): scaling limit of planar map decorated by uniform spanning tree
- CLE\(_{\kappa=6}\): scaling limit of critical percolation interfaces
on various domains (sphere, disk, ...)
SLE: Schramm-Lowener evolution
LQG: Liouville quantum gravity
CLE: conformal loop ensemble
spanning tree: subgraph without any cycle spanning all the vertices

Uniform spanning tree peano curve
by R. Lyons

Critical percolation interfaces
by S. Watson
Main Conjecture
\((M_n, P_n, Γ_n)\) converges under an appropriate scaling limit to an independent triple consisting of a \(\sqrt{2}\)-LQG sphere, a whole-plane SLE\(_8\) from \(\infty\) to \(\infty\), and a whole-plane CLE\(_6\).
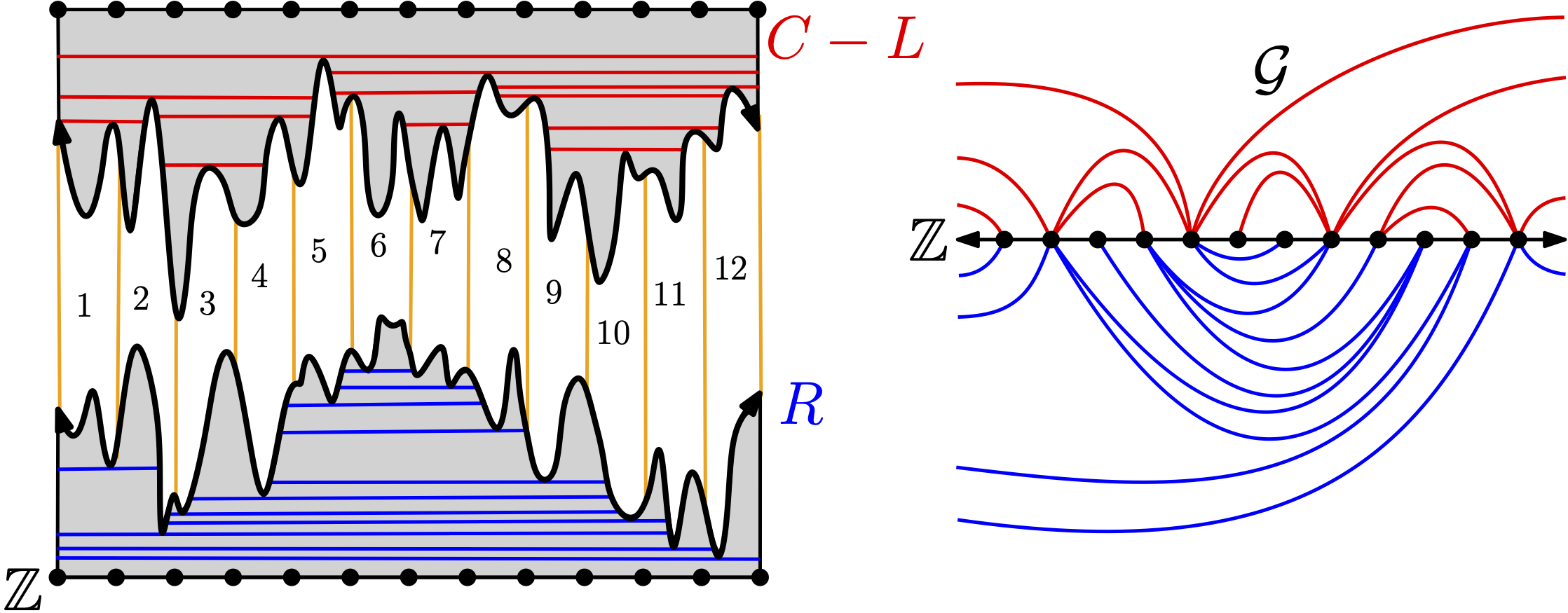
\(P_n\): Hamiltonian path on \(2n\) vertices
\(\Gamma_n\): Loops from two uniform arc diagrams
\(M_n\): Underlying planar map with \(2n\) vertices
LQG+SLE: mating of trees
\((M_n, P_n)\) is completely encoded by two independent uniform walk excursions, which converges to an independent pair of \(\sqrt{2}\)-LQG and SLE\(_8\) in the peanosphere sense
LQG+SLE: mating of trees

Tutte embedded Hamiltonian path on 500K points
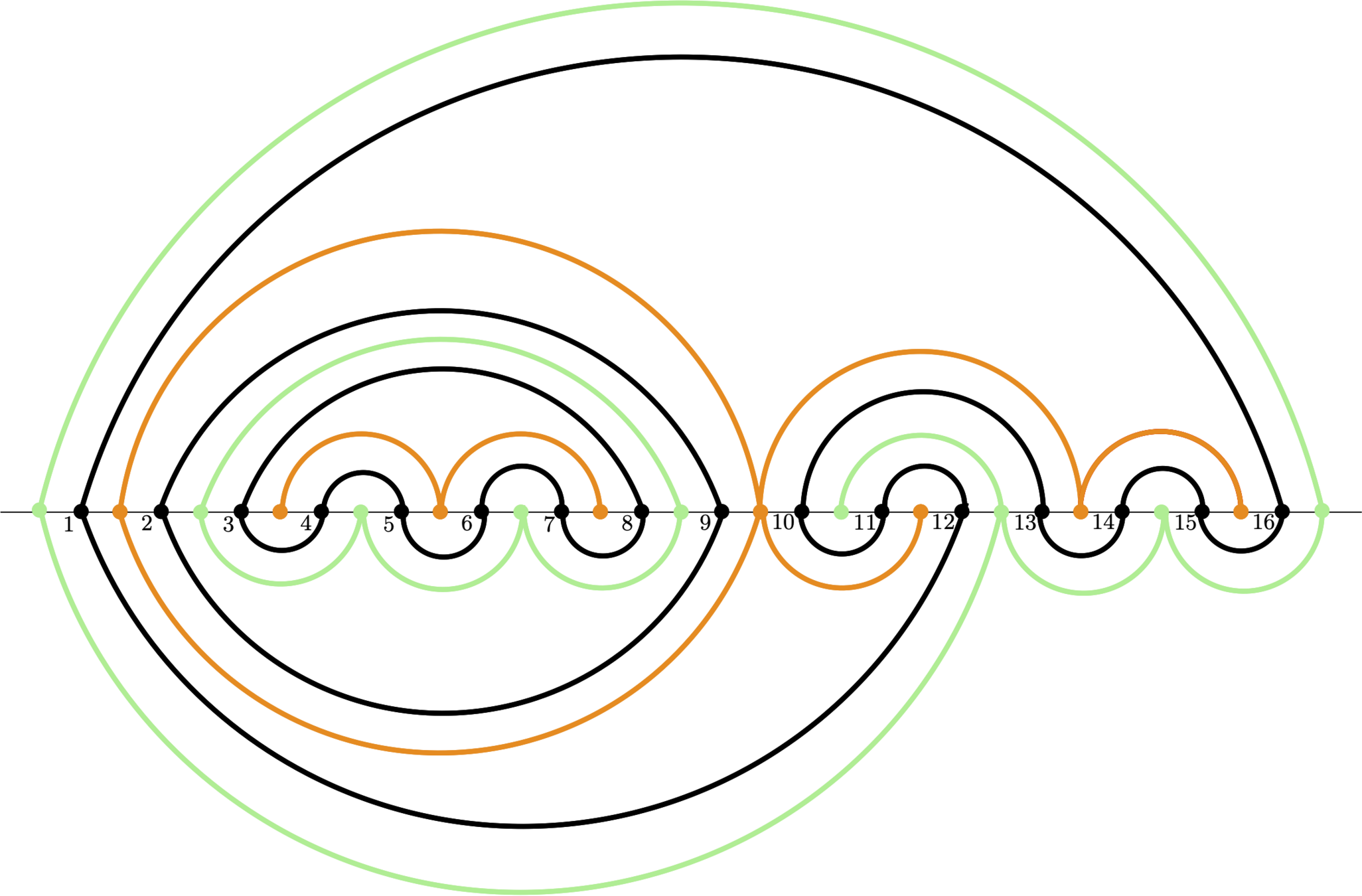
Loop ensemble
Tutte embedded loops
on 20K and 500K points
- The new part of the conjecture is CLE\(_6\)
- Motivated and justified by heuristic arguments ( Duplantier's talk, [DFGG], [BGS])
- If it is an independent CLE\(_\kappa\), then \(\kappa\) should be 6 whose central charge is 0
- Verified by several numerical simulations (growths of loop size, graph diameter, and crossing number)
Why CLE\(_6\)?
: Percolation analogy
For example, top-to-bottom open crossing in a box has probability 1/2, analogous to the critical percolation
The conjecture provides
a better understanding on geometry
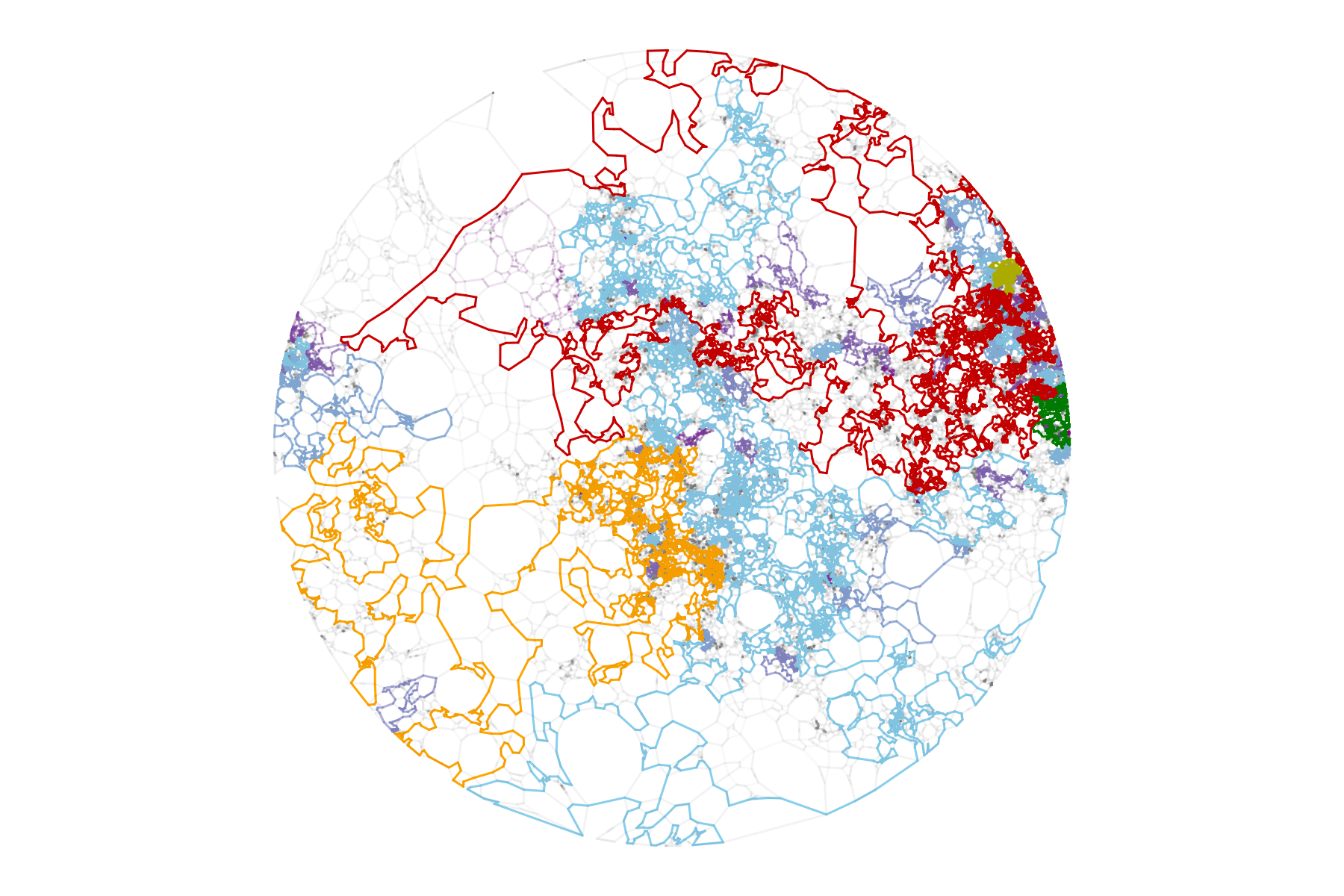
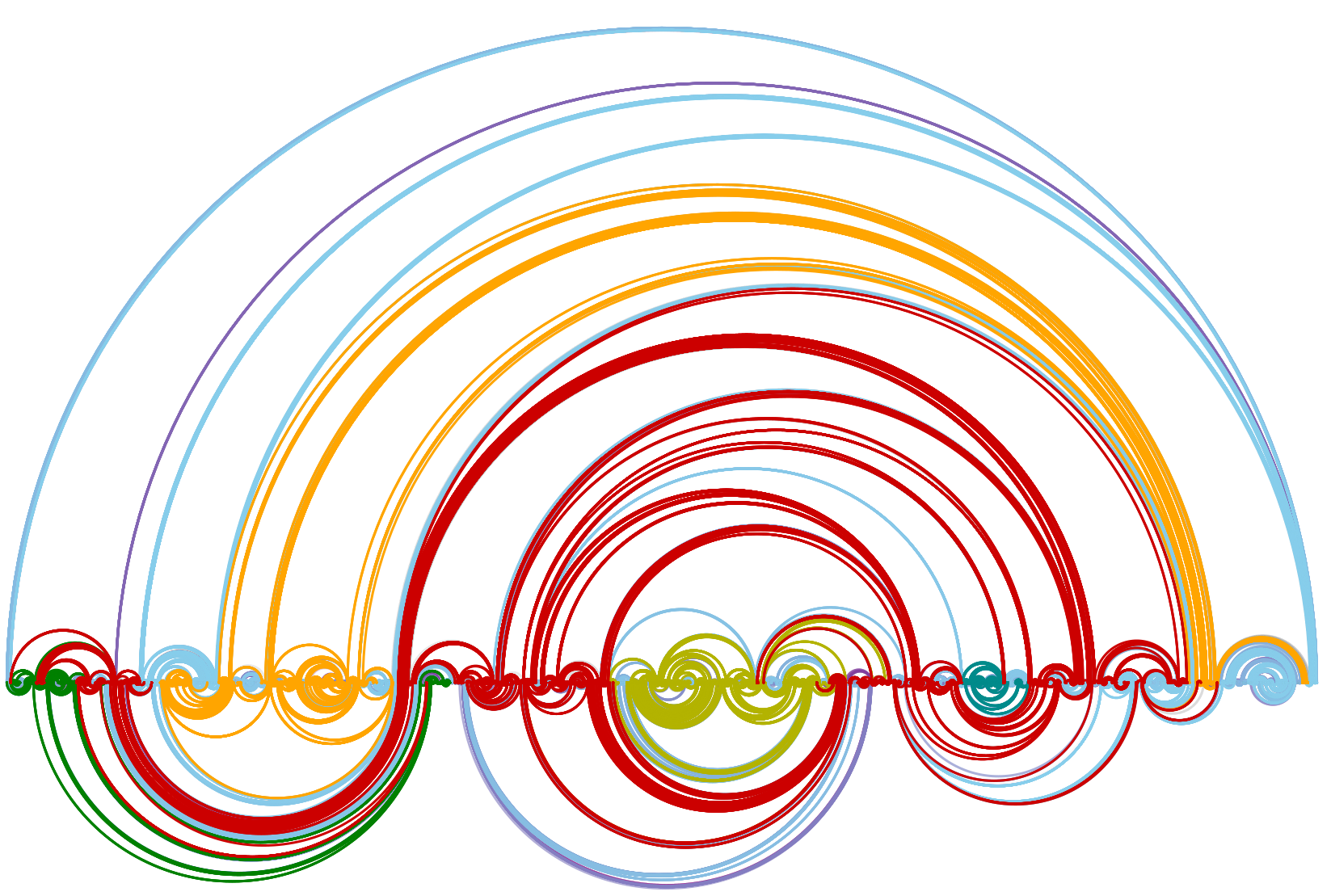
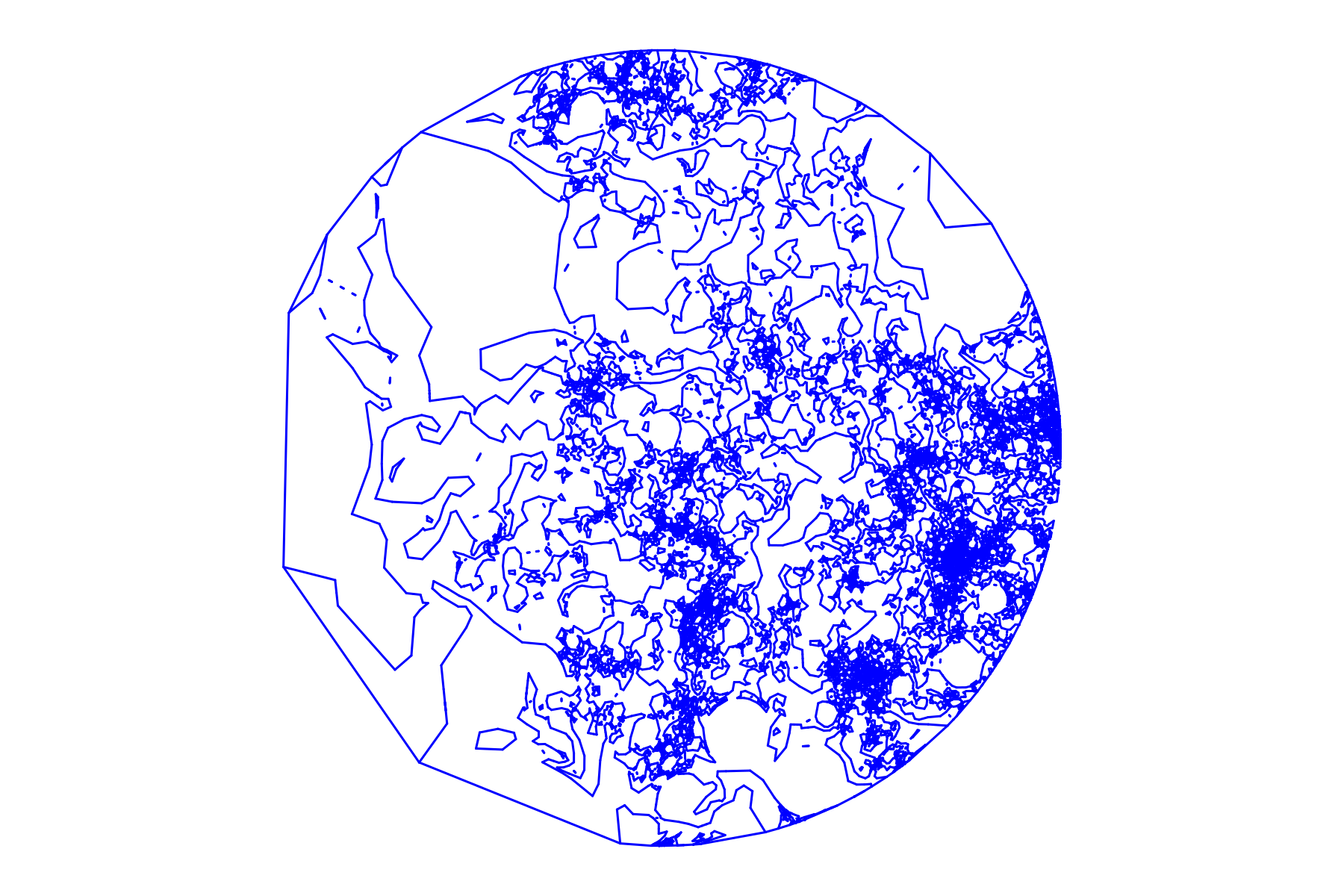
Uniform meandric system on 2M points with the first 300 largest loops colored
Kargin conjectured the largest loop size grows like \(n^{0.8}\) purely based on simulation
The size of largest loop
from Knizhnik-Polyakov-Zamolodchikov (KPZ) formula
\(\Delta_0\): Dimension w.r.t. Euclidean metric
\(\Delta_\gamma\): Dimension w.r.t. \(\gamma\)-LQG metric
Beffara computed the Euclidean dimension of SLE\(_6\) which equals to 7/4. Therefore, the \(\sqrt{2}\)-LQG dimension of CLE\(_6\) should be
For each fixed \(k\in\mathbb N\), \(\# \{\text{vertices of $k$th largest loop}\} = n^{\alpha + o(1)}\) with probability tending to \(1\) as \(n\to \infty\).
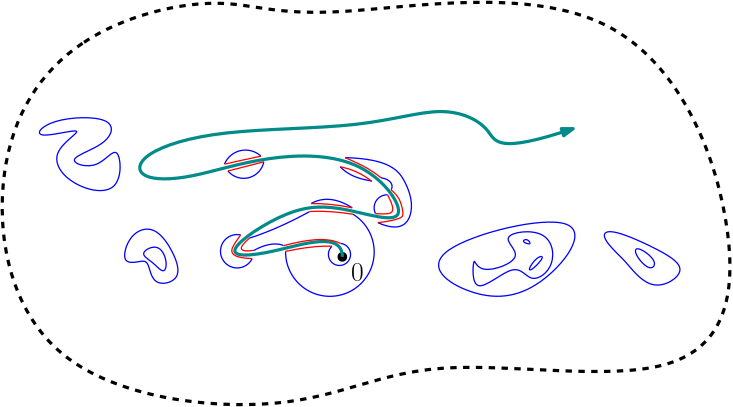
The non-existence of infinite path
in the uniform infinite meandric system
There is a.s. no infinite path in the uniform infinite meandric system.
Consider an infinite volume version of the uniform meandric system via Benjamini-Schramm local limit, studied in [CKST], [FT]
[CKST] proved that there is at most one infinite path in the uniform infinite meandric system.
\((M, P, Γ)\) converges under an appropriate scaling limit to an independent triple consisting of a \(\sqrt{2}\)-LQG cone, a whole-plane SLE\(_8\) from \(\infty\) to \(\infty\), and a whole-plane CLE\(_6\).
It is clear that this conjecture implies the non-existence of infinite path in the uniform infinite meandric system.
Rigorous results can be proven from
random planar map interpretation
\(\sqrt{2}\)-LQG cone
Recall that [DMS] provides a natural way to define a quantum surface with half-plane topology by cutting a whole-plane quatum surface with an independent SLE
✂️ whole-plane SLE\(_2\)
from 0 to \(\infty\)
\(\sqrt{2}\)-LQG wedge
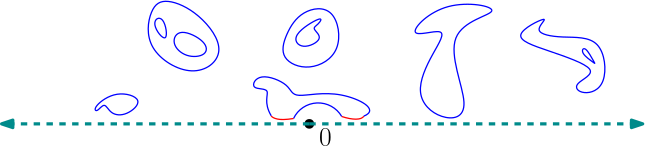
Uniform half-plane meandric system
There exists a.s. no infinite path in the uniform infinite half-plane meandric system. Furthermore, \(\frac12\) is diconnected from \(+\infty\) by infinitely many loops.
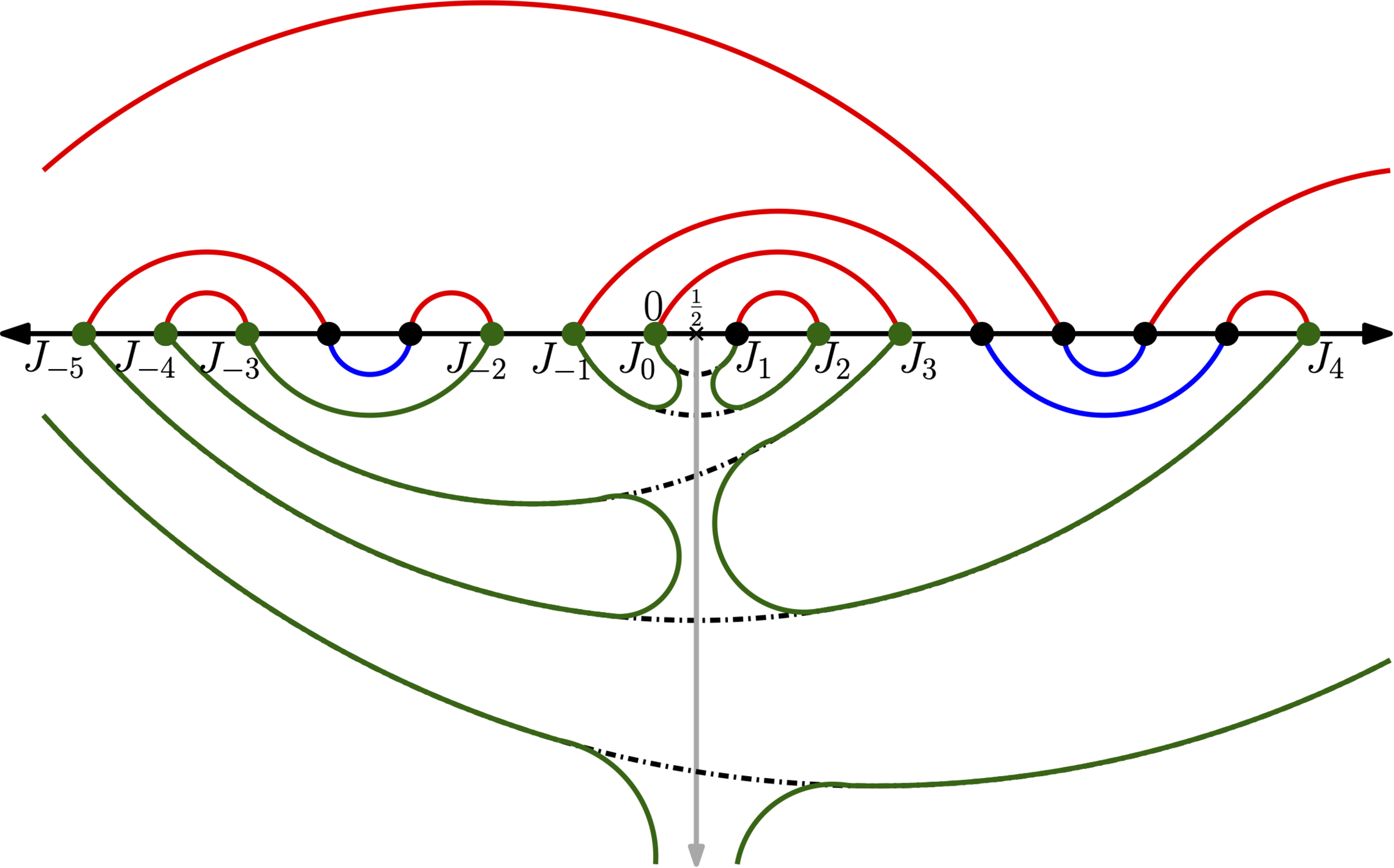
Proof is based on the Burton-Keane type argument.
Define the uniform (infinite) half-plane meandric system by cutting the bottom arcs of uniform meandric system with the ray \(\{\frac{1}{2}\}\times (-\infty,0)\)
Existence of macroscopic loops
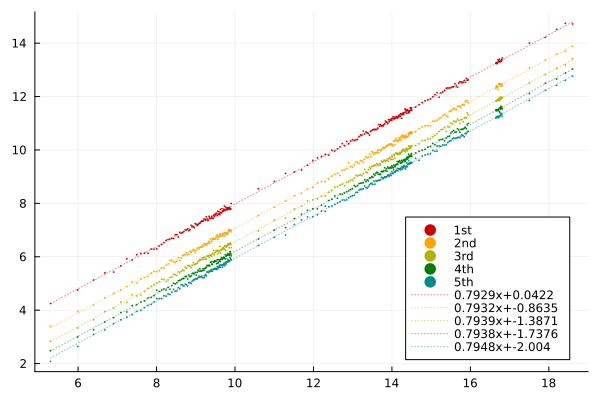
The graph distance diameter of \(M_n\) grows like \(n^{\frac{1}{d}-o(1)}\) as \(n\to \infty\).
\(d = \) Hausdorff dimension of \(\sqrt{2}\)-LQG satisfying \(3.55\le d\le 3.63\), so \(1/d\approx 0.28\)
The graph distance diameter of the largest loop grows like \(n^{\frac{1}{d}-o(1)}\) as \(n\to \infty\) which is of the same order with the entire map.
Therefore, the size of largest loop is at least \(n^{1/d-o(1)}\), not optimal at all compared to \(n^\alpha\), but much better than the trivial lower bound \(O(\log n)\) stated in Kargin.
Analogous to [CGHP] and [DCGPS]
Macroscopic loops in \(O(n)\) loop model
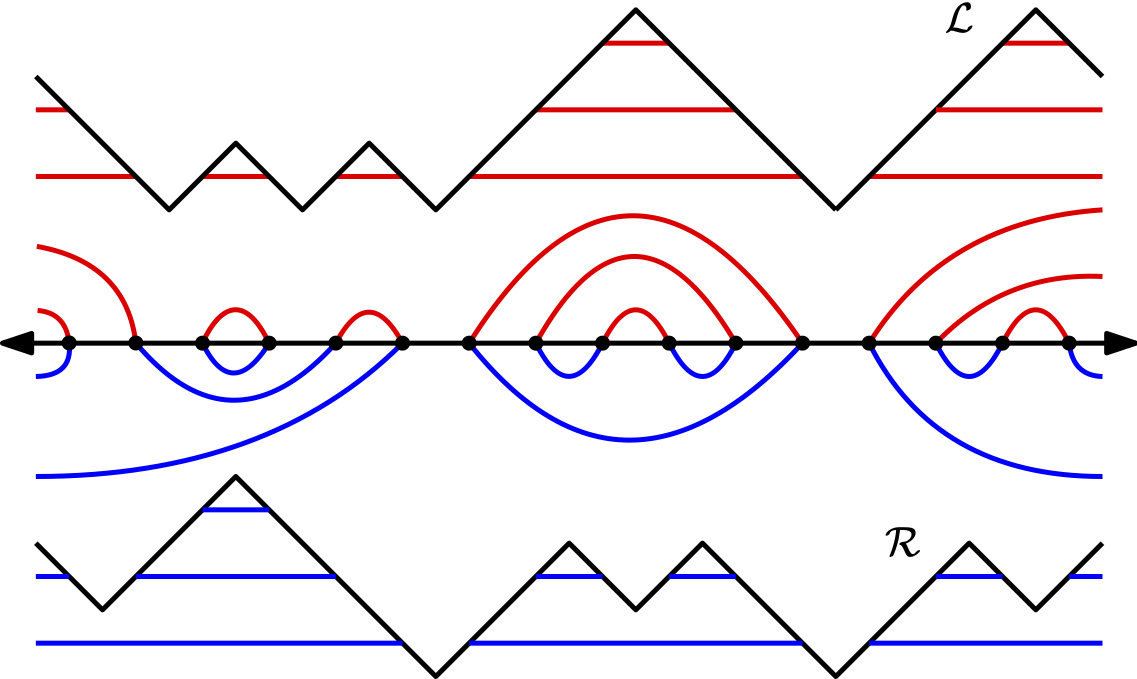
Comparison argument
For each \(\alpha > 0\), there exists \(A(\alpha) > 0\) and a coupling of \((L,R)\) with \((\mathcal L , \mathcal R)\) such that the following is true with probability \(1-O(n^{-\alpha})\):
\[A^{-1} (\log n)^{-3} \text{dist}_{\mathcal G}(x , y) \leq \text{dist}_{\mathcal M}(x , y) \leq A (\log n)^3 \text{dist}_{\mathcal G}(x , y).\]
\((L,R)\): two independent random walks encoding the uniform meandric system \(\mathcal M\)
\((\mathcal{L}, \mathcal{R})\): two independent Brownian motions encoding the mated-CRT map \(\mathcal{G}\)
Then, compare the mated-CRT map with LQG, where plenty of tools and standard LQG/SLE techniques are available.
Summary
- Our main conjecture is supported by heuristic arguments in physics and numerical evidence.
- In addition, the conjecture suggests new questions and natural variants of uniform meandric systems.
- By adopting a random geometry viewpoint, we are able to prove rigorous results on uniform meandric systems, such as the existence of macroscopic loops.
Open questions
- Prove conjectures
- Any notion of monotonicity and FKG-type inequalities?
- Interesting variants with different \(\kappa\) values
- Some bijections on meanders which allows a similar analysis presented here
Thank you!

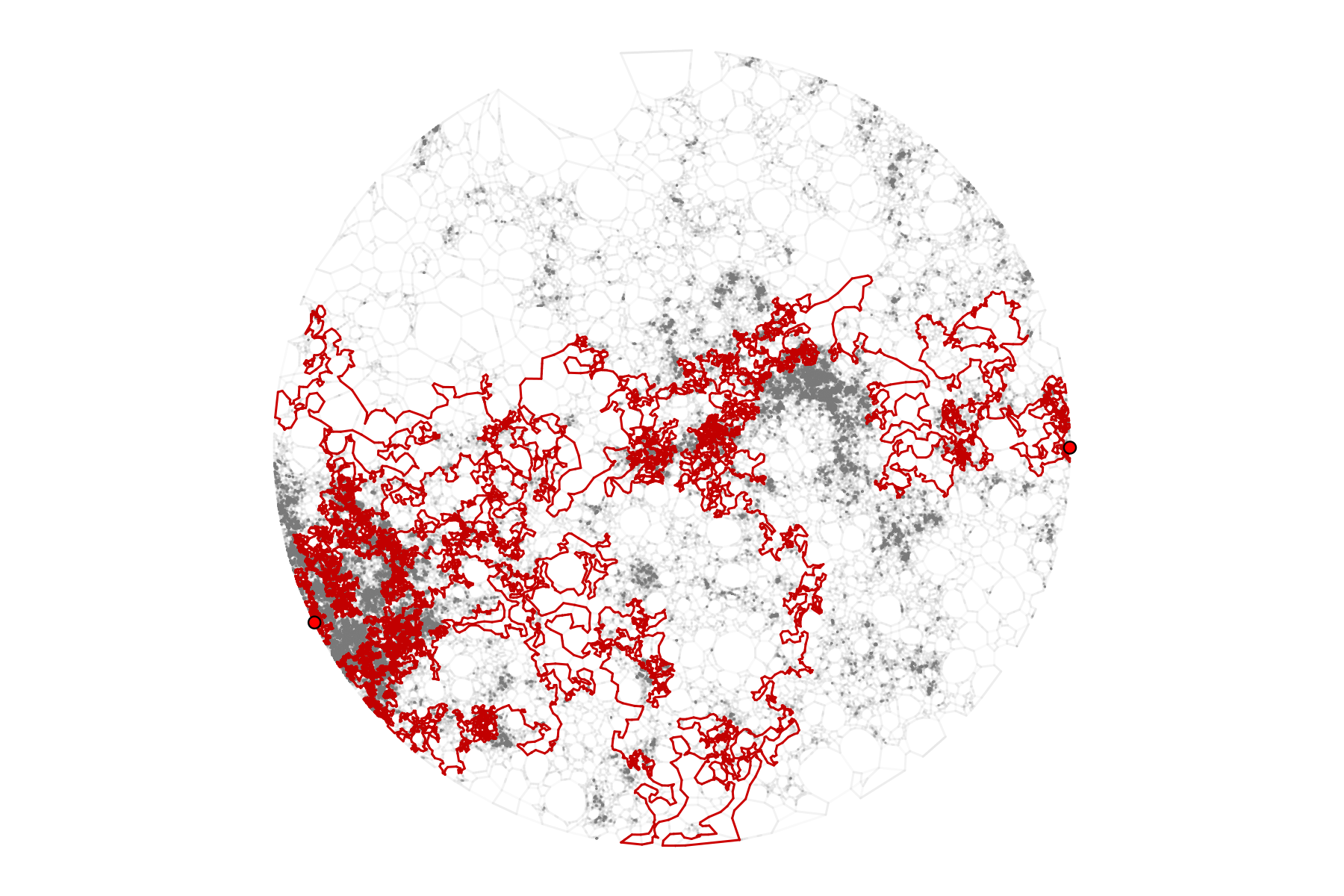
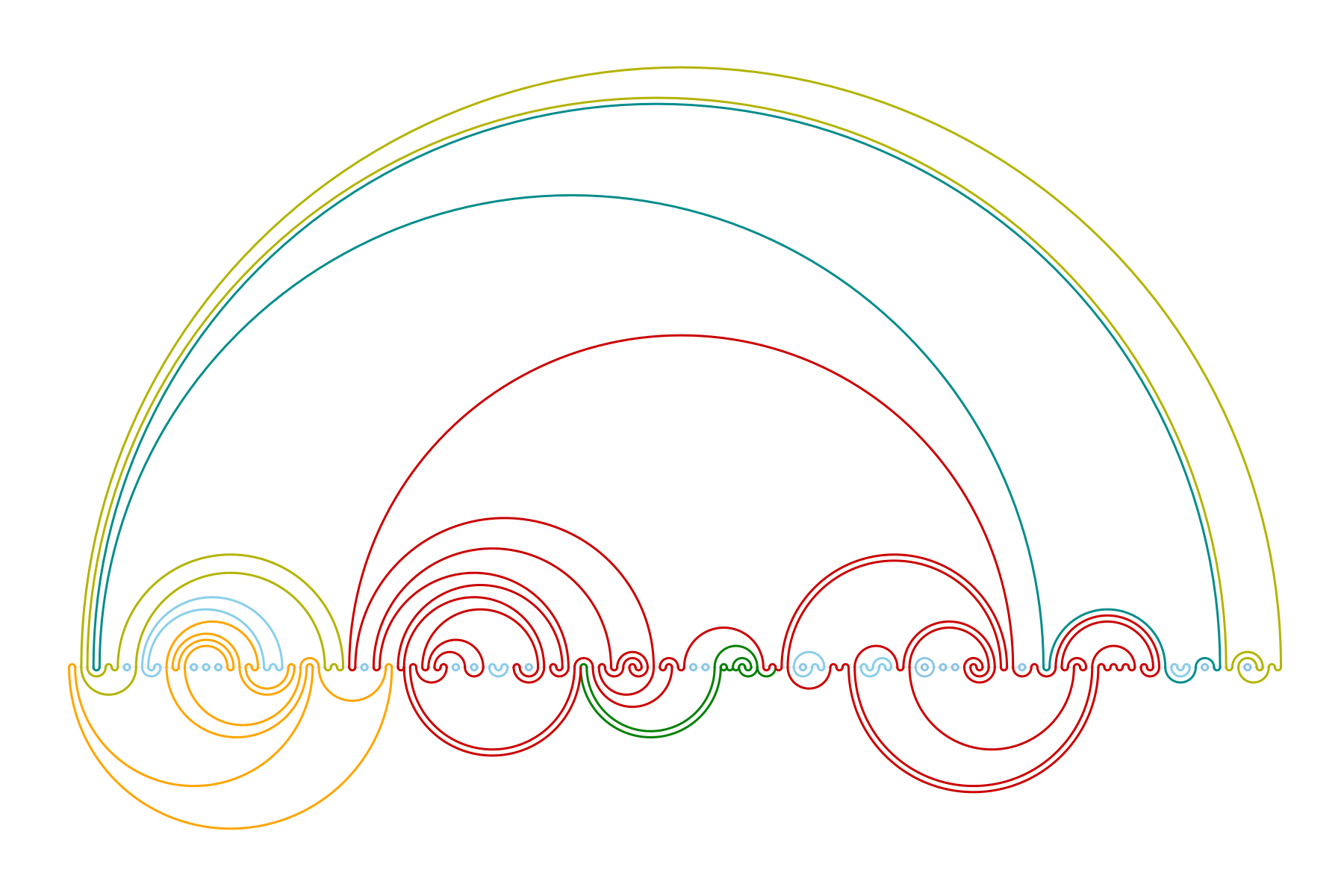
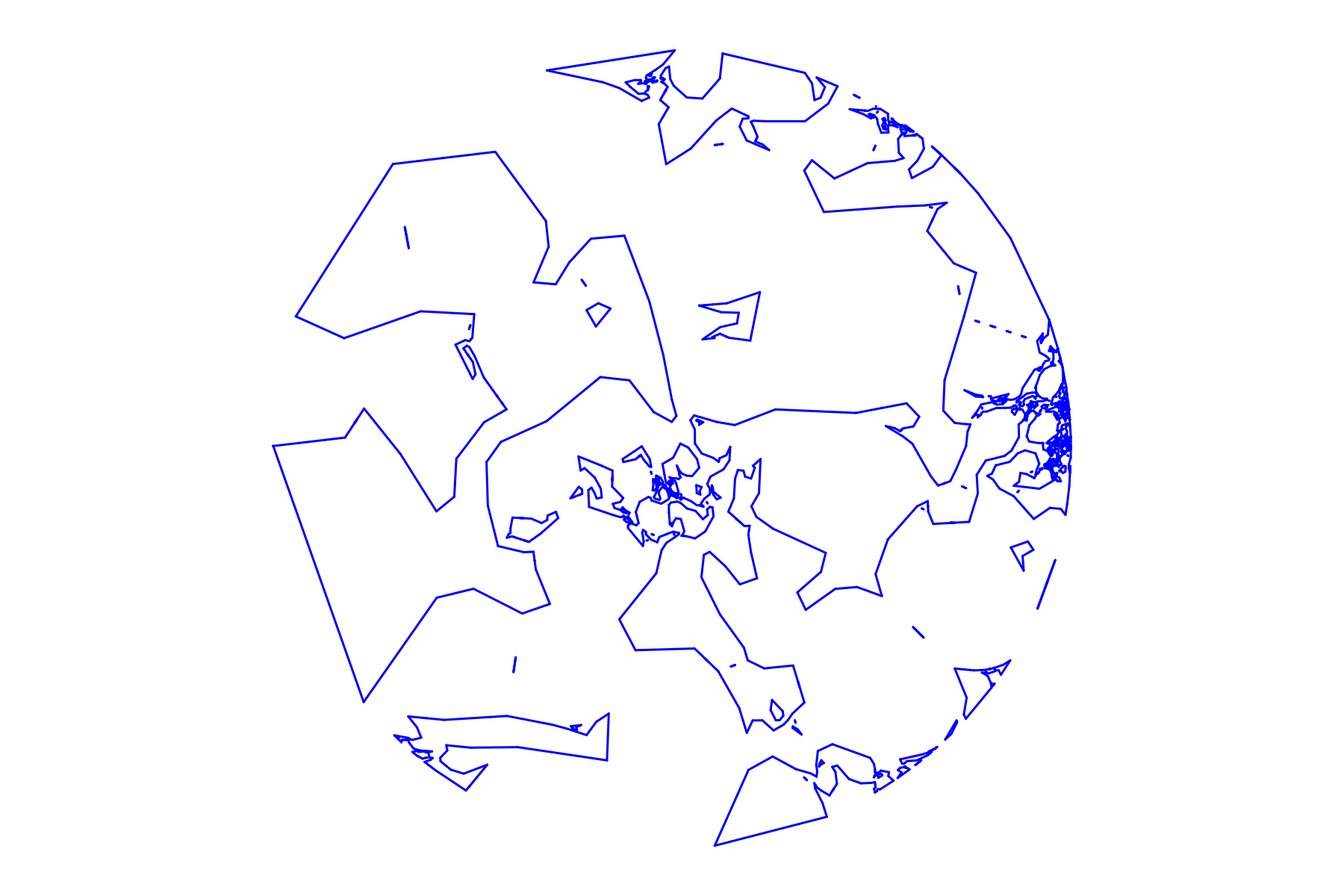
Concatenation of boundary loops on 18M points,
whose scaling limit should be SLE\(_6\)